Function Notation

Section 10.1 Function Notation

Objective: Identify functions and use correct notation to evaluate functions at numerical and variable values.

There are many different types of equations that we can work with in algebra. An equation gives the relationship between variables and numbers. Examples of several relationships are below:

\begin{equation*} \frac{(x+3)^2}{9}-\frac{(y+2)^2}{4}=1 \text{ and } y=x^2-2x+7 \text{ and } \sqrt{y+x}-7=xy \end{equation*}

There is a special classification of relationships known as functions. Functions have at most one output for any input. Generally $x$ is the variable that we plug into an equation and evaluate to find $y\text{.}$ For this reason $x$ is considered an input variable and $y$ is considered an output variable. This means the definition of a function, in terms of equations in $x$ and $y$ could be said, for any $x$ value there is at most one $y$ value that corresponds with it.

A great way to visualize this definition is to look at the graphs of a few relation- ships. Because $x$ values are vertical lines we will draw a vertical line through the graph. If the vertical line crosses the graph more than once, that means we have too many possible $y$ values. If the graph crosses the graph only once, then we say the relationship is a function.

Example 10.1.1.

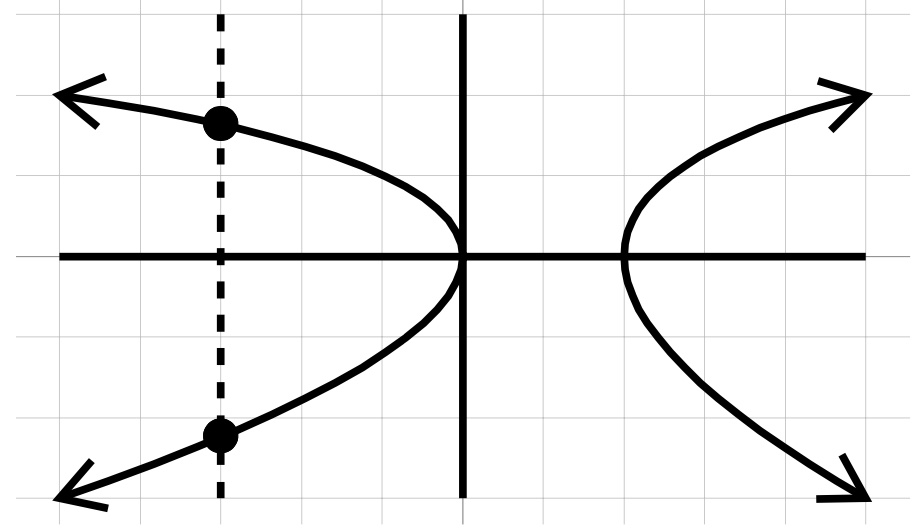
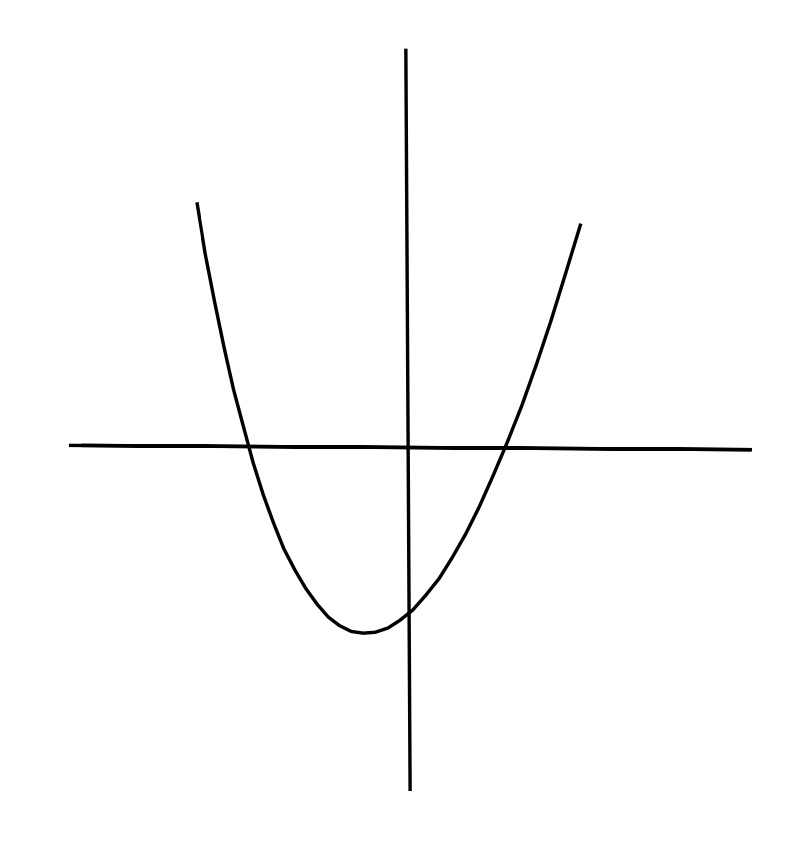
Which of the following graphs are graphs of functions?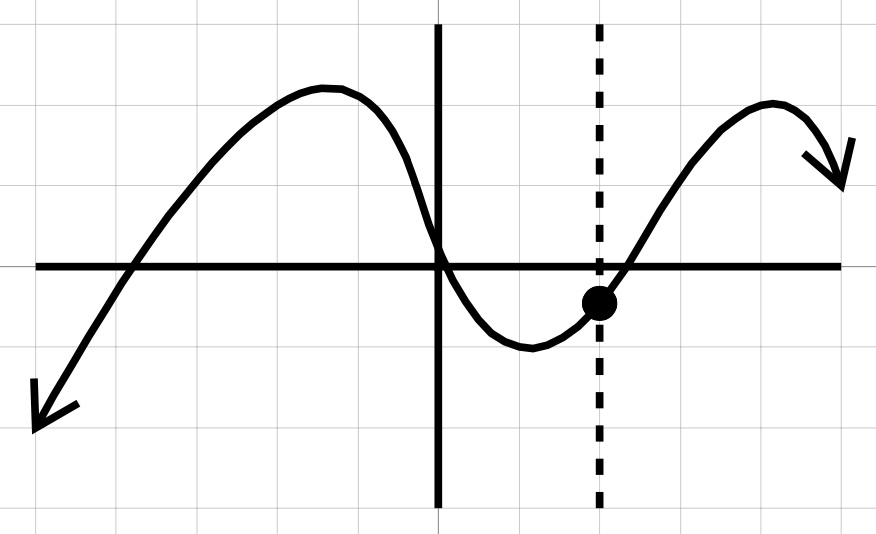

Drawing a vertical line through this graph will only cross the graph once, it is a function.

Drawing a vertical line through this graph will cross the graph twice, once at top and once at bottom. This is not a function.

Drawing a vertical line through this graph will cross the graph only once, it is a function.

We can look at the above idea in an algebraic method by taking a relationship and solving it for $y\text{.}$ If we have only one solution then it is a function.

Example 10.1.2.

\begin{align*} \text{Is } 3x^2-y=5 \text{a function?} \amp \quad \text{ Solve the relation for }y \\ -3x^2 \qquad -3x^2 \qquad\quad \amp\quad \text{Subtract $3x^2$ from both sides} \\ -y=-3x^2+5 \amp\quad \text{Divide each term by }-1 \\ \overline{-1} \qquad \overline{-1} \quad \overline{-1} \amp\quad \\ y=3x^2-5 \amp\quad \text{Only one solution for }y. \\ \text{Yes!}\amp\quad \text{It is a function} \end{align*}

Example 10.1.3.

\begin{align*} \text{Is } y^2-x=5 \text{ a function?} \amp \quad \text{Solve the relation for } y \\ +x \quad +x \qquad \qquad \amp \quad \text{Add $x$ to both sides}\\ y^2=x+5 \amp \quad \text{Square root of both sides}\\ \sqrt{y^2}=\pm \sqrt{x+5} \amp \quad \text{Simplify} \\ y=\pm \sqrt{x+5} \amp \quad \text{Two solutions for $y$ (one $+$, one $-$)} \\ \text{No! } \amp \quad \text{Not a function} \end{align*}

Once we know we have a function, often we will change the notation used to emphasis the fact that it is a function. Instead of writing $y=\text{,}$ we will use function notation which can be written $f(x)=\text{.}$ We read this notation “$f$ of “$x$” So for the above example that was a function, instead of writing $y = 3x^2-5\text{,}$ we could have written $f(x)=3x^2-5\text{.}$ It is important to point out that $f(x)$ does not mean $f$ times $x\text{,}$ it is merely a notation that names the function with the first letter (function $f$) and then in parenthesis we are given information about what variables are in the function (variable $x$). The first letter can be anything we want it to be, often you will see $g(x)$ (read $g$ of $x$).

World View Note: The concept of a function was first introduced by Arab mathematician Sharaf al-Din al-Tusi in the late 12th century

Once we know a relationship is a function, we may be interested in what values can be put into the equations. The values that are put into an equation (generally the $x$ values) are called the domain. When finding the domain, often it is easier to consider what cannot happen in a given function, then exclude those values.

Example 10.1.4.

\begin{align*} \text{Find the domain:} f(x)=\frac{3x-1}{x^2+x-6} \amp \quad \text{ With fractions, zero can't be in denominator} \\ x^2+x-6 \neq 0 \amp\quad \text{Solve by factoring} \\ (x+3)(x-2) \neq 0 \amp\quad \text{Set each factor not equal to zero} \\ x+3 \neq 0 \text{ and } x-2 \neq 0 \amp\quad \text{Solve each equation } \\ -3 -3 \quad \quad \ +2 +2 \amp\quad \\ x \neq -3,2 \amp\quad \text{Our Solution} \end{align*}

The notation in the previous example tells us that x can be any value except for $-3$ and $2\text{.}$ If $x$ were one of those two values, the function would be undefined.

Example 10.1.5.

\begin{align*} \text{Find the domain:} f(x)=3x^2-x \amp \quad \text{ With this equation there are no bad values} \\ \text{All the Real Numbers or } \mathbb{R} \amp\quad \text{Our Solution} \end{align*}

In the above example there are no real numbers that make the function undefined. This means any number can be used for $x\text{.}$

Example 10.1.6.

\begin{align*} \text{Find the domain: } f(x)=\sqrt{2x-3} \amp \quad \text{ Square roots can't be negative} \\ 2x-3 \geq 0 \amp\quad \text{ Set up an inequality } \\ +3 +3 \amp\quad \text{ Solve } \\ 2x \geq 3\amp\quad \text{ Solve } \\ \overline{2} \qquad \overline{2}\amp\quad \text{ Solve } \\ x \geq \frac{3}{2} \amp\quad \text{Our Solution } \end{align*}

The notation in the above example states that our variable can be $\frac{3}{2}$ or any number larger than $\frac{3}{2}\text{.}$ But any number smaller would make the function undefined (without using imaginary numbers).

Another use of function notation is to easily plug values into functions. If we want to substitute a variable for a value (or an expression) we simply replace the vari- able with what we want to plug in. This is shown in the following examples.

Example 10.1.7.

\begin{align*} f(x)=3x^2-4x; \text{ find } f(-2) \amp \quad \text{Substitute $-2$ in for $x$ in the function } \\ f(-2)=3(-2)^2-4(-2) \amp\quad \text{Evaluate, exponents first} \\ f(-2)=3(4)-4(-2) \amp\quad \text{Multiply} \\ f(-2)=12+8 \amp\quad \text{Add} \\ f(-2)=20 \amp\quad \text{Our Solution } \end{align*}

Example 10.1.8.

\begin{align*} h(x)=3^{2x-6}; \text{ find } h(4) \amp\quad \text{Substitute $4$ in for $x$ in the function} \\ h(3)=3^{2(4)-6} \amp\quad \text{Simplify exponent, multiplying first} \\ h(3)=3^{8-6} \amp\quad \text{Subtract in exponent} \\ h(3)=3^{2} \amp\quad \text{Evaluate exponent} \\ h(4)=9 \amp\quad \text{Our Solution} \end{align*}

Example 10.1.9.

\begin{align*} k(a)=2|a+4|;\text{ find } k(-7) \amp\quad \text{Substitute $-7$ in for $a$ in the function}\\ k(-7)=2|-7+4| \amp\quad \text{Add inside absolute values }\\ k(-7)=2|-3| \amp\quad \text{Evaluate absolute value } \\ k(-7)=2(3) \amp\quad \text{Multiply}\\ k(-7)=6 \amp\quad \text{Our Solution } \end{align*}

As the above examples show, the function can take many different forms, but the pattern to evaluate the function is always the same, replace the variable with what is in parenthesis and simplify. We can also substitute expressions into functions using the same process. Often the expressions use the same variable, it is important to remember each variable is replaced by whatever is in parenthesis.

Example 10.1.10.

\begin{align*} g(x)=x^4+1; \text{ find } g(3x) \amp \quad \text{Replace $x$ in the function with $(3x)$ } \\ g(3x)=(3x)^4+1 \amp\quad \text{Simplify exponent} \\ g(3x)=81x^4+1 \amp\quad \text{ Our Solution} \end{align*}

Example 10.1.11.

\begin{align*} p(t)=t^2-t; \text{ find } p(t+1) \amp \quad \text{Replace each $t$ in $p(t)$ with } (t+1) \\ p(t+1)=(t+1)^2-(t+1) \amp\quad \text{Square binomial } \\ p(t+1)=t^2+2t+1-(t+1) \amp\quad \text{Distribute negative } \\ p(t+1)=t^2+2t+1-t-1 \amp\quad \text{Combine like terms} \\ p(t+1)=t^2+t \amp\quad \text{Our Solution } \end{align*}

It is important to become comfortable with function notation and how to use it as we transition into more advanced algebra topics.

Exercises Exercises – Function Notation

Exercise Group.

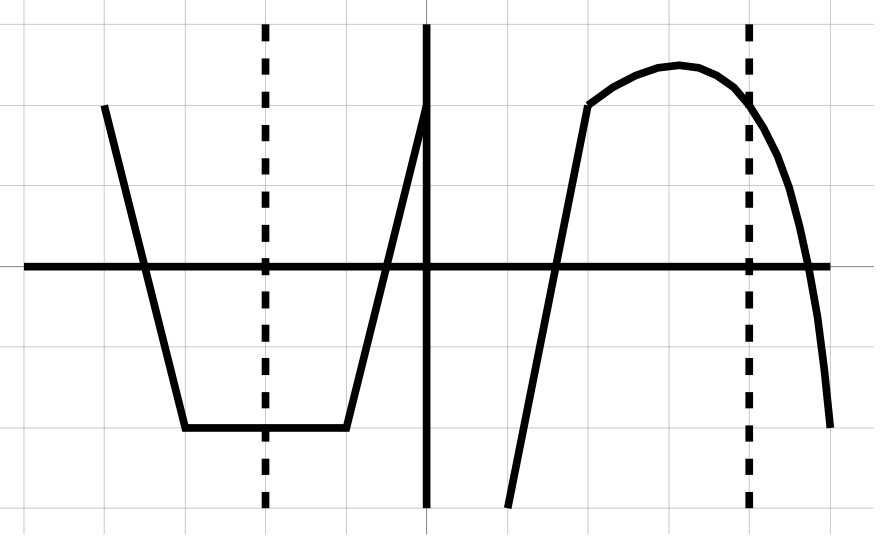
Solve. Which of the following is a function?

1.

2.

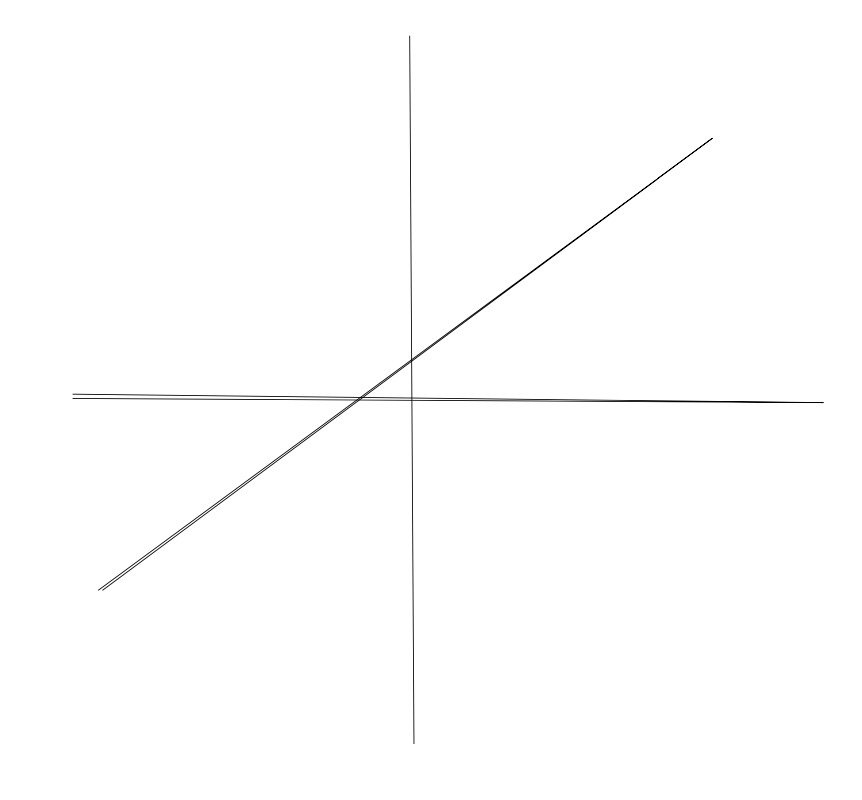
3.

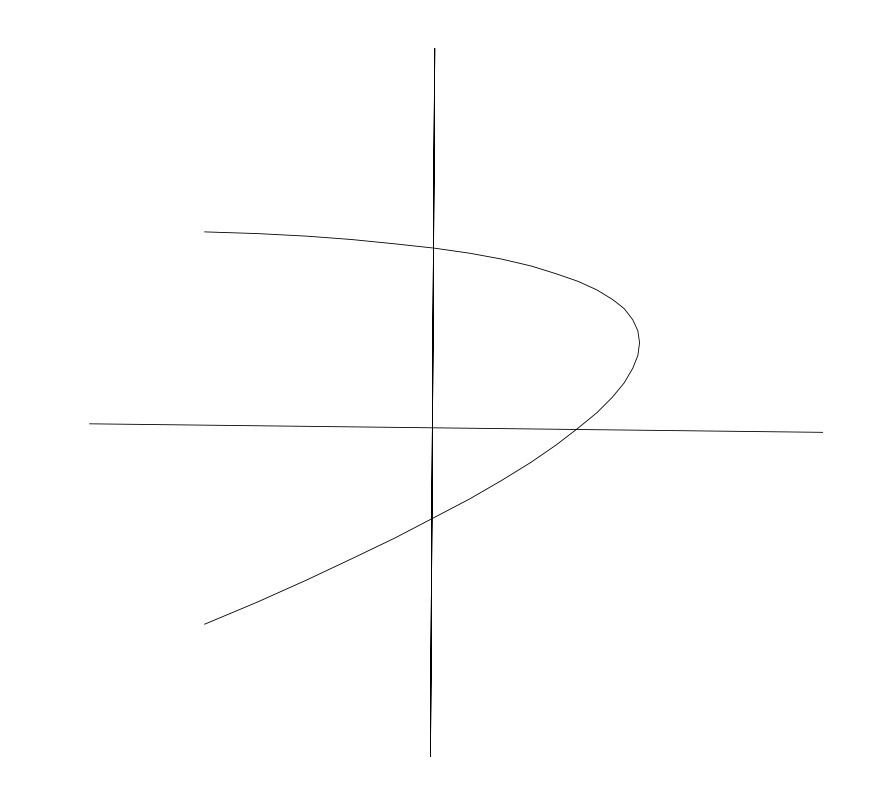
4.

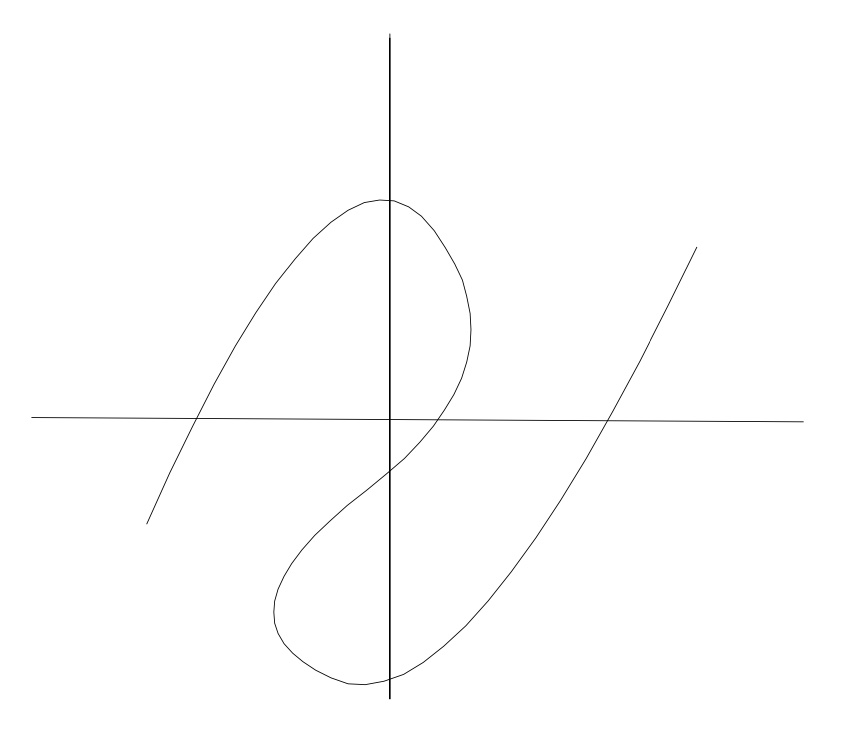
5.

$y=3x-7 $

6.

$\sqrt{y}+x=2 $

7.

$y^2-x^2=1$

8.

$x^2+y^2=1$

Exercise Group.

Specify the domain of each of the following functions.

9.

$f(x)=-5x+1 $

10.

$f(x)=\sqrt{5-4x} $

11.

$s(t)=\frac{1}{t^2}$

12.

$f(x)=x^2-3x-4 $

13.

$s(t)=\frac{1}{t^2+1}$

14.

$f(x)=\sqrt{x-16} $

15.

 f(x)=\frac{-2}{x^2-3x-4}

16.

$h(x)=\frac{\sqrt{3x-12}}{x^2-25} $

17.

$y(x)=\frac{r}{x^2-25} $

Exercise Group.

Evaluate each function.

18.

$g(x)4x-4;$ Find $g(0)$

19.

$g(n)=-3*5^{-n};$ Find $g(2)$

20.

$f(x)=-2|-n-2|+1;$ Find $f(-6)$

21.

$f(n)=n-3;$ Find $f(10)$

22.

$f(t)3^t-2;$ Find $f(-2)$

23.

$f(a)=3^{a-1};$ Find $f(2)$

24.

$f(t)=|t+3|;$ Find $f(10)$

25.

$w(x)=x^2+4x;$ Find $>w(-5)$

26.

$w(n)=2^{n+2};$ Find $w(-2)$

27.

$w(x)=-4+3;$ Find $w(6)$

28.

$p(n)=-3|n|;$ Find $p(7)$

29.

$k(a)=a+3;$ Find $k(-1)$

30.

$p(t)=-t^3+t;$ Find $p(4)$

31.

$k(x)=-2*4^{2x-2};$ Find $k(2)$

32.

$k(n)=|n-1|;$ Find $k(3)$

33.

$p(t)=-2*4^{2t+1}; $ >Find $p(-2)$

34.

$h(x)=x^3+2;$ Find $h(-4x)$

35.

$h(n)=4n+2;$ Find $h(n+2)$

36.

$h(x)=3x+2;$ Find $h(-1+x)$

37.

$-3*2^{a+3};$ Find $h(\frac{a}{4})$

38.

$h(t)=2|-3t-1|+2;$ Find $h(n^2)$

39.

$h(x)=x^2+1;$ Find $h(\frac{x}{4})$

40.

$g(x)=5^{x};$ Find $g(3x)$

41.

$h(t)=t^2+t;$ Find $h(t^2)$

42.

$g(x)=5^x;$ Find $g(-3-x)$

43.

$h(n)=5^{n-1};$ Find $h(\frac{n}{2})$