Section 9.9 Quadratics - Graphs of Quadratics
Just as we drew pictures of the solutions for lines or linear equations, we can draw a picture of solution to quadratics as well. One way we can do that is to make a table of values.
Example 9.9.1.
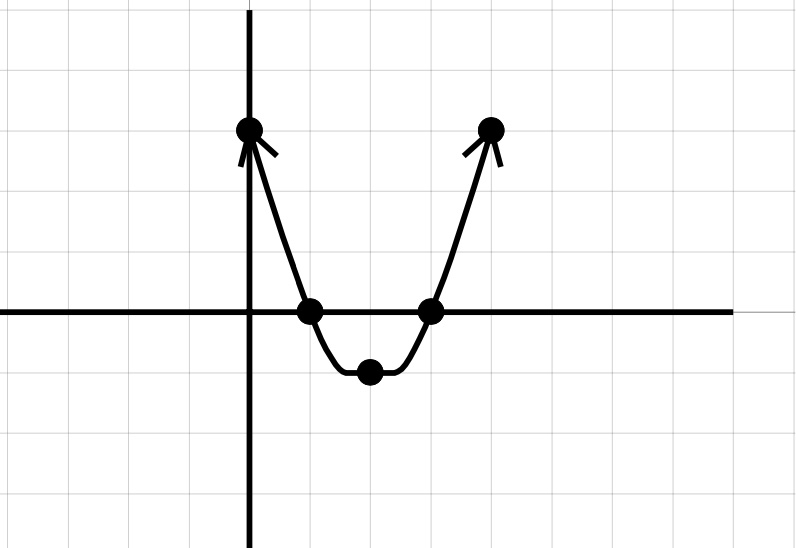
Plot the points \((0, 3)\text{,}\) \((1, 0)\text{,}\) \((2, - 1)\text{,}\) \((3, 0)\text{,}\) and \((4, 3)\text{.}\)
Connect the dots with a smooth curve.
Our Solution
When we have \(x^2\) in our equations, the graph will no longer be a straight line. Quadratics have a graph that looks like a U shape that is called a parabola.
World View Note: The first major female mathematician was Hypatia of Egypt who was born around 370 AD. She studied conic sections. The parabola is one type of conic section.
The above method to graph a parabola works for any equation, however, it can be very tedious to find all the correct points to get the correct bend and shape. For this reason we identify several key points on a graph and in the equation to help us graph parabolas more efficiently. These key points are described below.
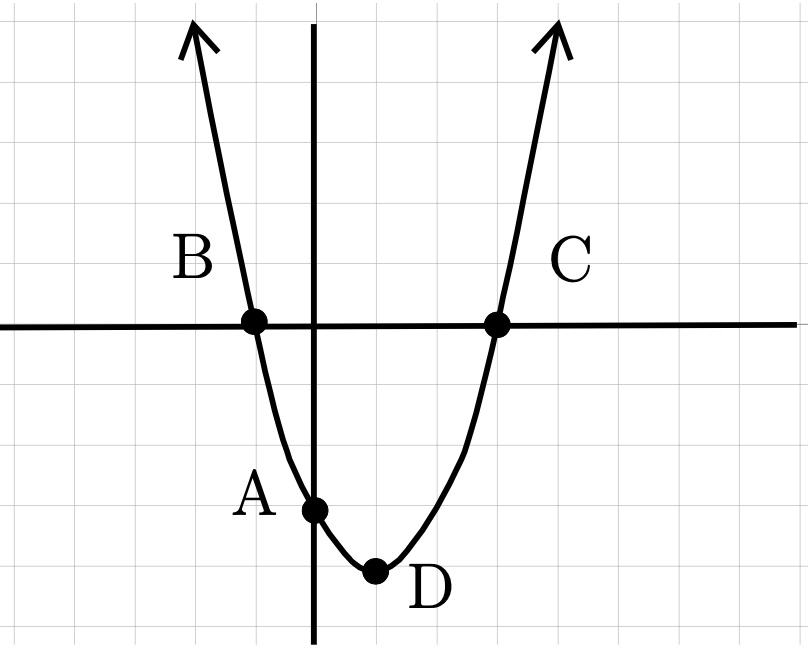
Point \(A:\) \(y\)-intercept: Where the graph crosses the vertical \(y\)-axis.
Points \(B\) and \(C:\) \(x\)-intercepts: Where the graph crosses the horizontal \(x\)-axis
Point \(D:\) Vertex: The point where the graph curves and changes directions.
We will use the following method to find each of the points on our parabola.
To graph the equation \(y=ax^2+bx+c \text{,}\) find the following points
\(y\)-intercept: Found by making \(x = 0 \text{,}\) this simplifies down to \(y = c \)
\(x\)-intercepts: Found by making \(y = 0 \text{,}\) this means solving \(0 = ax^2+bx+c \)
Vertex: Let \(x = \frac{-b}{2a}\) to find \(x\text{.}\) Then plug this value into the equation to find \(y \text{.}\)
After finding these points we can connect the dots with a smooth curve to find our graph!
Example 9.9.2.
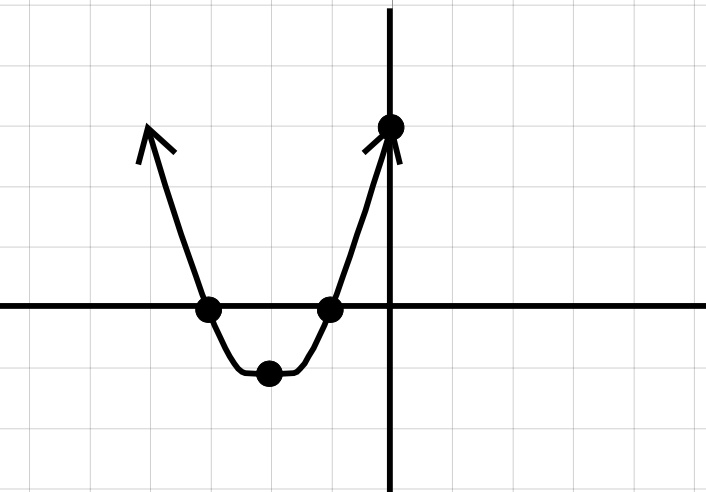
Graph the\(y\)-intercept at \(3\text{,}\) the \(x\)- intercepts at \(-3\) and \(-1\text{,}\) and the vertex at \((-2, -1). \text{.}\) Connect the dots with a smooth curve in a U shape to get our parabola.
Our Solution
If the a in \(y=ax^2 +bx+c \) is a negative value, the parabola will end up being an upside-down U. The process to graph it is identical, we just need to be very careful of how our signs operate. Remember, if \(a\) is negative, then \(ax^2 \) will also be negative because we only square the \(x \text{,}\) not the \(a\text{.}\)
Example 9.9.3.
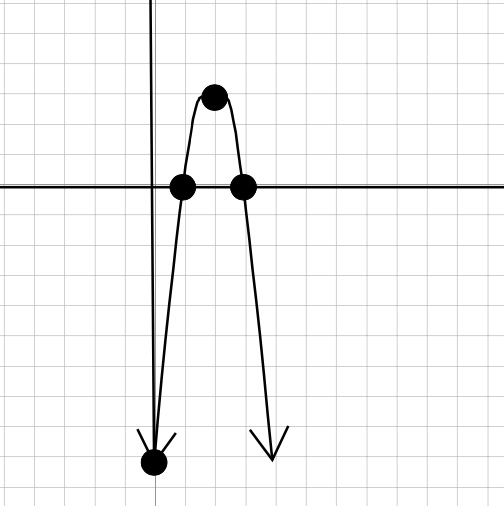
Graph the y-intercept at \(-9\text{,}\) the \(x\)- intercepts at \(3\) and \(1\text{,}\) and the vertex at \((2, 3)\text{.}\) Connect the dots with smooth curve in an upside-down U shape to get our parabola.
Our Solution
It is important to remember the graph of all quadratics is a parabola with the same U shape (they could be upside-down). If you plot your points and we cannot connect them in the correct U shape then one of your points must be wrong. Go back and check your work to be sure they are correct!
Just as all quadratics (equation with \(y = x^2\)) all have the same U-shape to them and all linear equations (equations such as \(y = x\)) have the same line shape when graphed, different equations have different shapes to them. Below are some common equations (some we have yet to cover!) with their graph shape drawn.
| Absolute Value | Cubic |
| \(y=|x|\) | \(y=x^3\) |
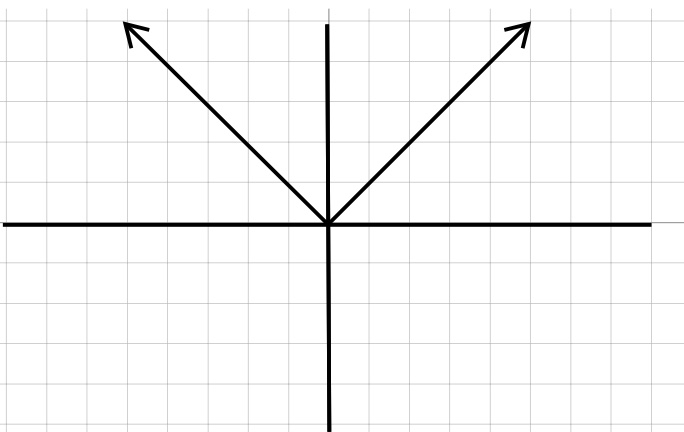 |
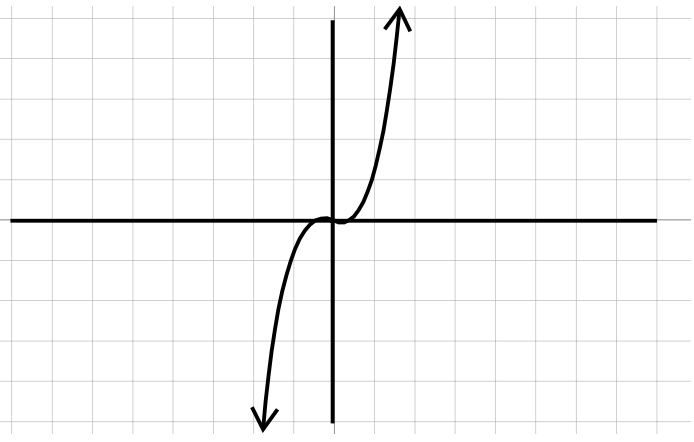 |
| Quadratic | Exponential |
| \(y=x^2\) | \(y=a^x\) |
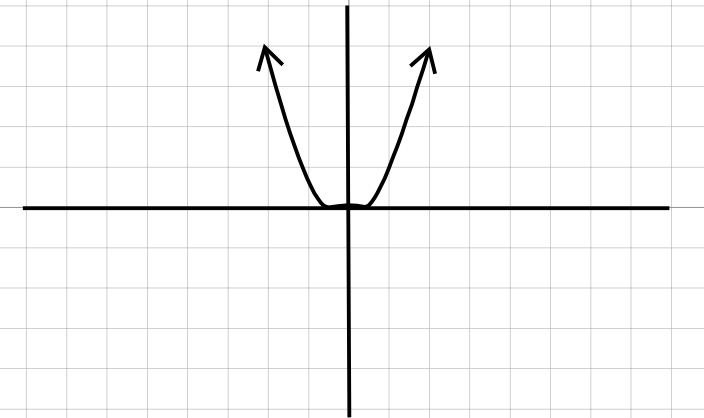 |
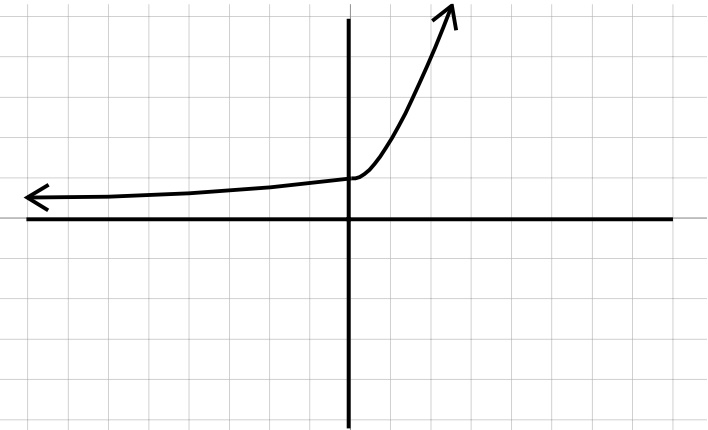 |
| Square Root | Logarithmic |
| \(y=/sqrt{x}\) | \(y=\log_{a}x\) |
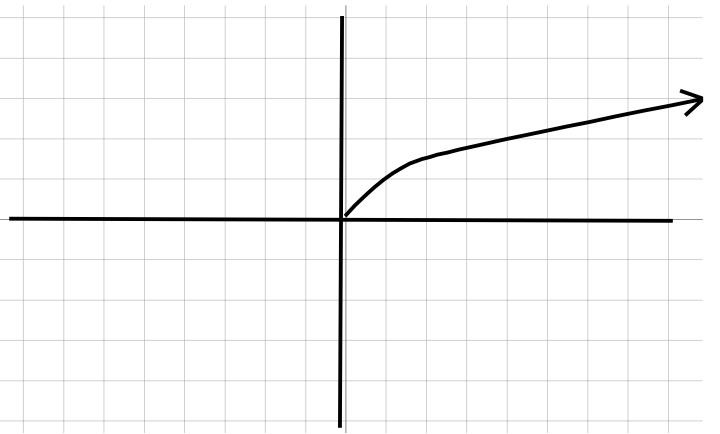 |
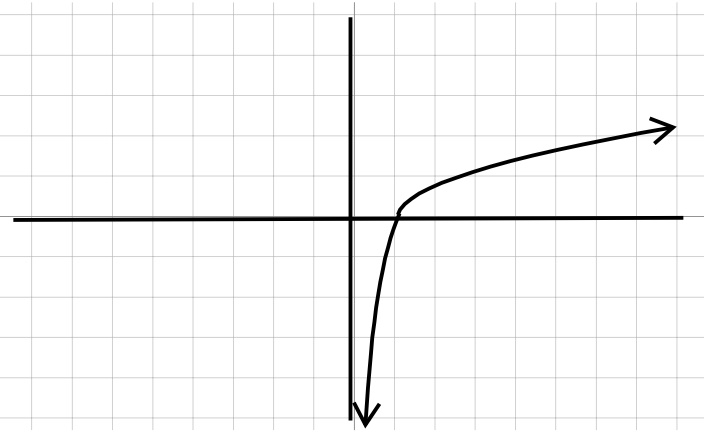 |
Exercises Exercises - Graphs of Quadratics
Exercise Group.
Find the vertex and intercepts of the following quadratics. Use this information to graph the quadratic.
1.
\(y=x^2-2x-8 \)
2.
\(y=x^2-2x-3 \)
3.
\(y=2x^2-12x+10 \)
4.
\(y=2x^2-12x+16 \)
5.
\(y=-2x^2+12x-18 \)
6.
\(y=-2x^2+12-10 \)
7.
\(y=-3x^2+24x-45 \)
8.
\(y=-3x^2+12x-9\)
9.
\(y=-x+4x+5 \)
10.
\(y=-3x^2+4x-3 \)
11.
\(y=-x^2+6x-5\)
12.
\(y=-2x^2+16x-30 \)
13.
\(y=-2x^2+16x-24 \)
14.
\(y=2x^2+4x-6 \)
15.
\(y=3x^2+12x+9 \)
16.
\(y=5x^2+30+45 \)
17.
\(y=5x^2-40x+75 \)
18.
\(y=5x^2+20x+15 \)
19.
\(y=-5x^2-60x-175 \)
20.
\(y=-5x^2+20x-15 \)