Slope-Intercept Form

Section 2.3 Slope-Intercept Form

Objective: Give the equation of a line with a known slope and y-intercept.

When graphing a line, we found one method we could use is to make a table of values. However, if we can identify some properties of the line, we may be able to make a graph much quicker and easier. One such method is finding the slope and the y-intercept of the equation. The slope can be represented by m and the y-intercept, where it crosses the axis and $x = 0$ , can be represented by $(0, b) $ where b is the value where the graph crosses the vertical y-axis. Any other point on the line can be represented by $(x, y) \text{.}$ Using this information, we will look at the slope formula and solve the formula for $y\text{.}$

Example 2.3.1.

\begin{align*} m,(0, b),(x, y) \amp \quad \text{ Using the slope formula gives: } \\ \frac{y-b}{x-0} =m \amp\quad \text{ Simplify } \\ \frac{y-b}{x} =m \amp\quad \text{ Multiply both sides by } x \\ y- b = mx \amp \quad \text{ Add $b$ to both sides } \\ + b \quad + b \amp\quad \text{ } \\ y = mx + b \amp\quad \text{ Our Solution } \end{align*}

This equation, $y = mx + b$ can be thought of as the equation of any line that as a slope of m and a y-intercept of$b$ . This formula is known as the slope-intercept equation.

Slope - Intercept Equation: $y = mx + b$

If we know the slope and the y-intercept we can easily find the equation that represents the line.

Example 2.3.2.

\begin{align*} \text{ Slope }= \frac{3}{4} , y - \text{intercept }= -3\amp \quad \text{ Use the slope - intercept equation } \\ y = mx + b \amp\quad \text{ $m$ is the slope, $ b$ is the y - intercept } \\ y = \frac{3}{4} x -3 \amp\quad \text{ Our Solution } \end{align*}

We can also find the equation by looking at a graph and finding the slope and y-intercept.

Example 2.3.3.

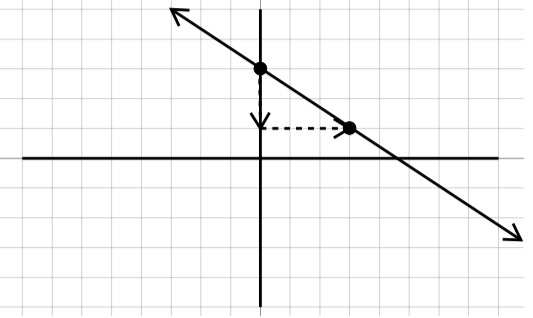
Identify the point where the graph crosses the $y$-axis $(0,3)\text{.}$ This means the $y$-intercept is $3\text{.}$
Identify one other point and draw a slope triangle to find the slope. The slope is $-\frac{2}{3}\text{.}$
$y = mx + b$ Slope-intercept equation.
$y = -\frac{2 }{3} x + 3$ Our Solution

We can also move the opposite direction, using the equation identify the slope and y-intercept and graph the equation from this information. However, it will be important for the equation to first be in slope intercept form. If it is not, we will have to solve it for $y$ so we can identify the slope and the y-intercept.

Example 2.3.4.

\begin{align*} \text{Write in slope - intercept form: } 2x -4y = 6 \amp \quad \text{ Solve for } y \\ -2x \quad - 2x \amp\quad \text{ Subtract $2x$ from both sides } \\ - 4y = - 2x + 6 \amp\quad \text{Put $x $ term first } \\ \frac{-4y}{-4}=\frac {-2x}{-4}+\frac{6}{-4} \amp \quad \text{ Divide each term by } -4 \\ y = \frac{1}{ 2} x -\frac{3}{ 2} \amp\quad \text{ Our Solution } \end{align*}

Once we have an equation in slope-intercept form we can graph it by first plotting the y-intercept, then using the slope, find a second point and connecting the dots.

Example 2.3.5.

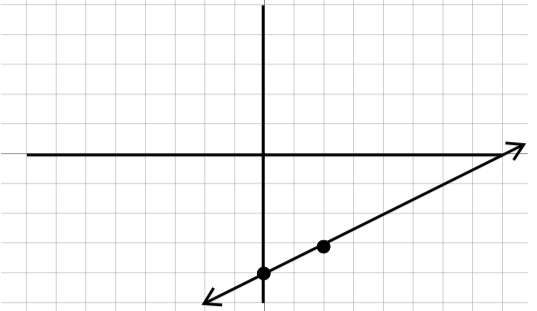
\begin{align*} \text{ Graph } y =\frac{1}{ 2} x -4 \amp \quad \text{ Recall the slope - intercept formula} \\ y = mx + b \amp\quad \text{ Identify the slope, $ m$, and the $y$– intercept,} b \\ m = \frac{1}{ 2} , b = -4 \amp\quad \text{Make the graph } \end{align*}

Starting with a point at the y-intercept of $-4\text{,}$
Then use the slope $\frac{ \text{rise} }{\text{run}}$ , so we will rise $1$ unit and run $2$ units to find the next point.
Once we have both points, connect the dots to get our graph.

World View Note: Before our current system of graphing, French Mathematician Nicole Oresme, in $1323 $ suggested graphing lines that would look more like a $103 $ bar graph with a constant slope!

Example 2.3.6.

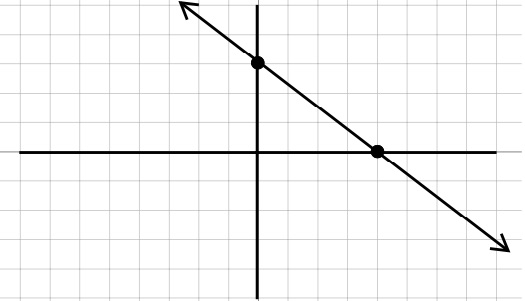
\begin{align*} \text{Graph } 3x + 4y = 12 \amp \quad \text{ Not in slope intercept form } \\ -3x \quad -3x \amp\quad \text{Subtract $3x$ from both sides } \\ 4y =- 3x + 12 \amp\quad \text{ Put the $x$ term first } \\ \frac{4y}{4}=\frac{-3x}{4}+\frac{12}{4} \amp \quad \text{ Divide each term by } 4 \\ y = -\frac{3 }{4} x + 3 \amp\quad \text{ Recall slope - intercept equation } \\ y = mx + b \amp\quad \text{ Identify $m$ and }b \\ m =-\frac{ 3}{ 4} , b = 3 \amp \quad \text{ Make the graph } \end{align*}

Starting with a point at the y-intercept of $3\text{,}$
Then use the slope $\frac{ \text{rise} }{\text{run}}$ , so we will drop $3$ unit and run $4$ units to find the next point.
Once we have both points, connect the dots to get our graph.

We want to be very careful not to confuse using slope to find the next point with use a coordinate such as $(4, - 2) $ to find an individual point. Coordinates such as $(4, - 2) $ start from the origin and move horizontally first, and vertically second. Slope starts from a point on the line that could be anywhere on the graph. The numerator is the vertical change and the denominator is the horizontal change.

Lines with zero slope or no slope can make a problem seem very different. Zero slope, or horizontal line, will simply have a slope of zero which when multiplied by $x $ gives zero. So, the equation simply becomes $y = b$ or $y $ is equal to the y-coordinate of the graph. If we have no slope, or a vertical line, the equation can’t be written in slope intercept at all because the slope is undefined. There is no y in these equations. We will simply make $x $ equal to the $x$-coordinate of the graph.

Example 2.3.7.

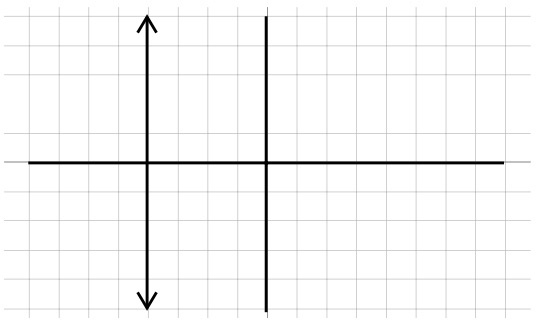
Give the equation of the line in the graph.
Because we have a vertical line and no slope there is no slope-intercept equation we can use. Rather we make $x$ equal to the $x$-coordinate of $-4$
$x = -4$ Our Solution

Exercises Exercises - Slope-Intercept Form

Exercise Group.

Write the slope-intercept form of the equation of each line given the slope and the y-intercept.

1.

$\text{Slope}= 2,\ y-\text{intercept}= 5 $

2.

$\text{Slope} =- 6,\ y-\text{intercept} = 4 $

3.

$\text{Slope} = 1,\ y-\text{intercept} = -4 $

4.

$\text{Slope} = - 1,\ y-\text{intercept} = -2 $

5.

$\text{Slope} =-\frac{3}{ 4} ,\ y-\text{intercept} = - 1 $

6.

$\text{Slope} =-\frac{1}{ 4} ,\ y-\text{intercept} = 3 $

7.

$\text{Slope} =\frac{ 1}{ 3} ,\ y-\text{intercept} = 1 $

8.

$\text{Slope} = \frac{2}{ 5} ,\ y-\text{intercept} = 5 $

Exercise Group.

Write the slope-intercept form of the equation of each line.

9.

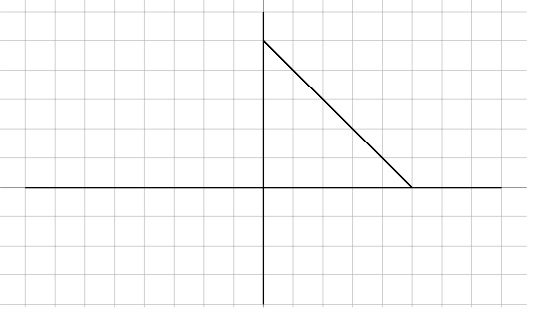
10.

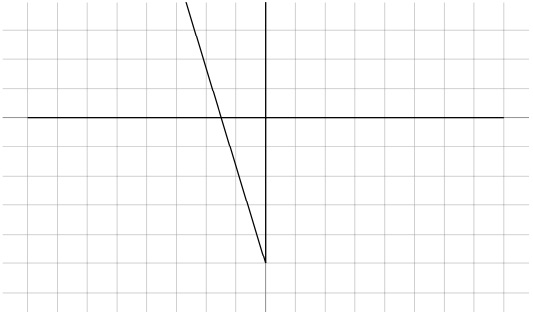
11.

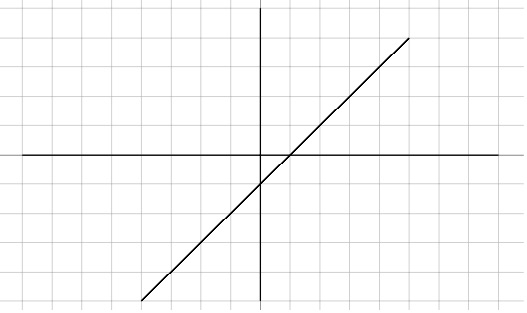
12.

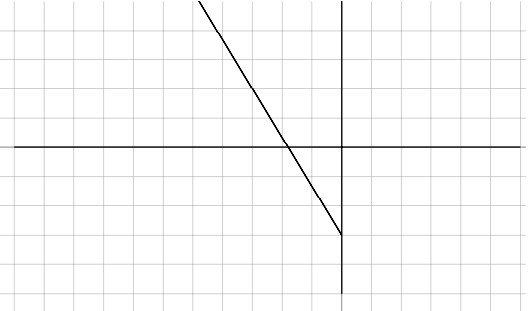
13.

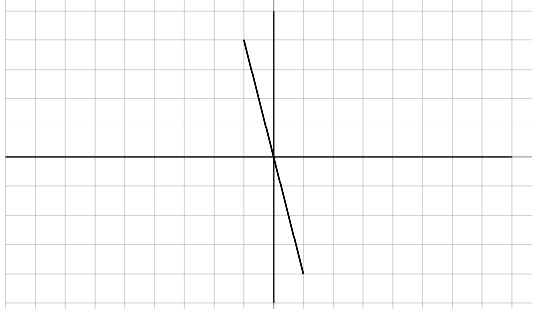
14.

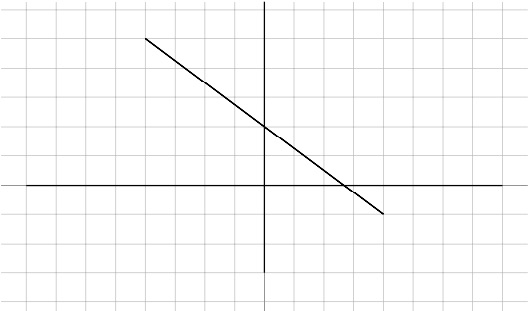
15.

$x + 10y = - 37 $

16.

$x - 10y = 3 $

17.

$2x + y = -1 $

18.

$6x - 11y = - 70 $

19.

$7x - 3y = 24 $

20.

$4x +7y = 28 $

21.

$x = -8 $

22.

$x-7y = -42 $

23.

$y - 4 = -(x + 5) $

24.

$y - 5 = \frac{5}{ 2} (x - 2) $

25.

$y - 4 =4(x - 1) $

26.

$y - 3 = -\frac{2}{3} (x +3) $

27.

$y + 5= - 4(x - 2) $

28.

$0= x -4 $

29.

$y + 1= -\frac{1}{ 2} (x - 4) $

30.

$y + 2= \frac{6}{ 5} (x +5) $

Exercise Group.

Sketch the graph of each line.

31.

$y = \frac{1}{ 3} x + 4 $

32.

$y =-frac{1}{ 5} x - 4 $

33.

$y =\frac{ 6}{ 5} x - 5 $

34.

$y =-\frac{ 3}{ 2} x - 1 $

35.

$y = \frac{3 }{2} x $

36.

$y = -\frac{3}{4} x + 1 $

37.

$x - y + 3= 0 $

38.

$4x +5= 5y $

39.

$-y- 4+ 3x = 0 $

40.

$- 8= 6x -2y $

41.

$- 3y = -5x + 9 $

42.

$- 3y =3 -\frac{3}{ 2} x $