Parallel and Perpendicular Lines

Section 2.5 Parallel and Perpendicular Lines

Objective: : Identify the equation of a line given a parallel or perpendicular line.

There is an interesting connection between the slope of lines that are parallel and the slope of lines that are perpendicular (meet at a right angle). This is shown in the following example.

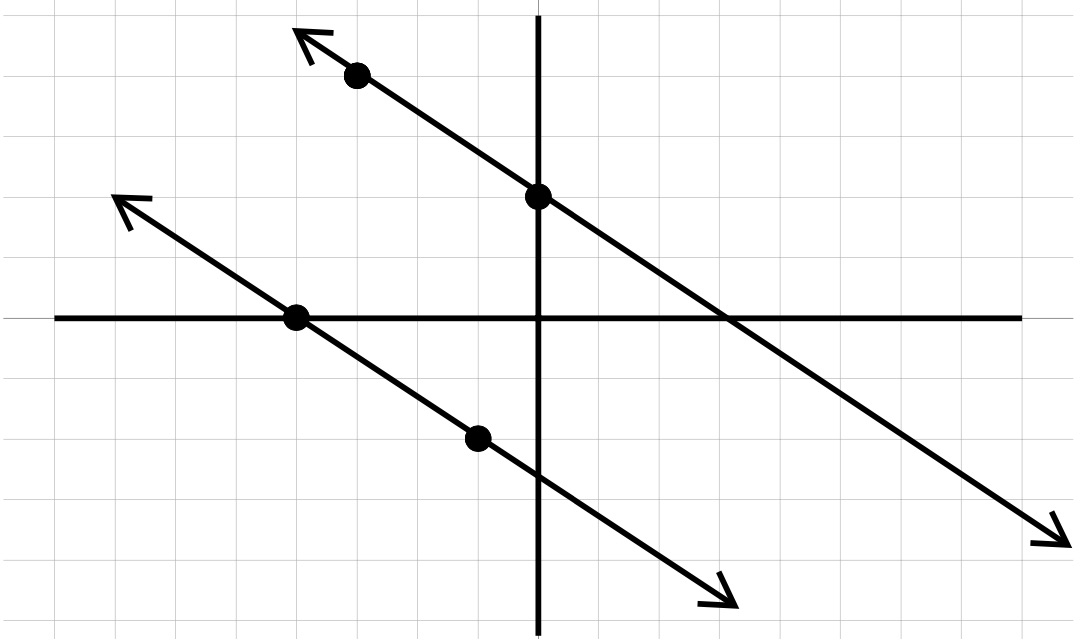
Example 2.5.1.

Figure 2.5.2. The above graph has two parallel lines. The slope of the top line is down $2\text{,}$ run $3\text{,}$ or $-\frac{2}{ 3}$ . The slope of the bottom line is down $2\text{,}$ run $3$ as well, or $-\frac{2}{ 3}\text{.}$

Figure 2.5.3. The above graph has two perpendicular lines. The slope of the flatter line is up $2\text{,}$ run $3$ or $\frac{2}{ 3}\text{.}$ The slope of the steeper line is down $3 \text{,}$ run $2 $ or $-\frac{ 3}{ 2} \text{.}$

World View Note: Greek Mathematician Euclid lived around $300$ BC and published a book titled, The Elements. In it is the famous parallel postulate which mathematicians have tried for years to drop from the list of postulates. The attempts have failed, yet all the work done has developed new types of geometries!

As the above graphs illustrate, parallel lines have the same slope and perpendicular lines have opposite (one positive, one negative) reciprocal (flipped fraction) slopes. We can use these properties to make conclusions about parallel and perpendicular lines

Example 2.5.4.

Find the slope of a line parallel to $5y - 2x = 7\text{.}$

\begin{align*} 5y - 2x =7 \amp \quad \text{ To find the slope we will put equation in slope - intercept form } \\ +2x + 2x \amp\quad \text{ Add $2x$ to both sides } \\ 5y = 2x +7 \amp\quad \text{ Put $x$ term first } \\ \frac{5y}{5}=\frac{2x+7}{5} \amp \quad \text{ Divide each term by } 5 \\ y =\frac{ 2}{ 5} x +\frac{ 7}{ 5} \amp\quad \text{ The slope is the coefficient of } x \\ m =\frac{ 2}{ 5} \amp\quad \text{ Slope of first line. Parallel lines have the same slope } \\ m = \frac{2}{5} \amp \quad \text{ Our Solution } \end{align*}

Example 2.5.5.

Find the slope of a line perpendicular to $3x - 4y = 2$

\begin{align*} 3x - 4y = 2\amp \quad \text{ To find slope we will put equation in slope - intercept form } \\ -3x \qquad - 3x \amp\quad \text{ Subtract $3x$ from both sides } \\ -4y = -3x + 2 \amp\quad \text{ Put x term first } \\ \frac{-4y}{-4}=\frac{-3x+2}{-4} \amp \quad \text{ Divide each term by } -4 \\ y = \frac{3}{ 4} x -\frac{ 1}{ 2} \amp\quad \text{ The slope is the coefficient of x } \\ m =\frac{ 3}{ 4} \amp\quad \text{Slope of firstlines. Perpendicular lines have opposite reciprocal slopes } \\ m = -\frac{ 4}{ 3} \amp \quad \text{ Our Solution } \end{align*}

Once we have a slope, it is possible to find the complete equation of the second line if we know one point on the second line.

Example 2.5.6.

Find the equation of a line through $(4, - 5) $ and parallel to $2x - 3y =6\text{.}$

\begin{align*} 2x -3y =6 \amp \quad \text{We first need slope of parallel line } \\ -2x \quad - 2x \amp\quad \text{ Subtract $2x$ from each side } \\ -3y = - 2x +6 \amp\quad \text{ Put $x$ term first } \\ \frac{-3y}{-3}=\frac{-2x+6}{-3} \amp \quad \text{ Divide each term by } -3\\ y =\frac{2} {3} x - 2 \amp\quad \text{Identify the slope, the coefficient of } x \\ m =\frac{2}{3} \amp\quad \text{Parallel lines have the same slope } \\ m =\frac{ 2}{ 3} \amp \quad \text{ We will use this slope and our point } (4, - 5) \\ y - y_1 = m(x -x_1) \amp\quad \text{ Plug this information into point slope formula } \\ y - ( - 5)= \frac{2 }{3} (x - 4) \amp\quad \text{ Simplify signs } \\ y +5=\frac{2}{ 3} (x - 4) \amp \quad \text{ Our Solution } \end{align*}

Example 2.5.7.

Find the equation of the line through $(6, - 9) $ perpendicular to $y = -\frac{3}{ 5} x + 4$ in slope-intercept form.

\begin{align*} y = -\frac{3}{ 5} x + 4 \amp \quad \text{ Identify the slope, coefficient of } x \\ m = -\frac{3}{ 5} \amp\quad \text{ Perpendicular lines have opposite reciprocal slopes } \\ m = \frac{5}{ 3} \amp\quad \text{ We will use this slope and our point } (6, - 9) \\ y - y_1 = m(x - x_1) \amp \quad \text{ Plug this information into point - slope formula } \\ y - ( -9) = \frac{5 }{3} (x - 6) \amp\quad \text{ Simplify signs } \\ y + 9=\frac{5}{ 3} (x - 6) \amp\quad \text{ Distribute slope } \\ y + 9= \frac{5}{ 3} x -10 \amp \quad \text{ Solve for } y \\ - 9 \qquad \quad -9 \amp\quad \text{ Subtract $9$ from both sides } \\ y =\frac{ 5}{ 3} x -19 \amp\quad \text{ Our Solution } \end{align*}

Zero slopes and no slopes may seem like opposites (one is a horizontal line, one is a vertical line). Because a horizontal line is perpendicular to a vertical line, we can say that no slope and zero slope are actually perpendicular slopes!

Example 2.5.8.

Find the equation of the line through $(3, 4) $ perpendicular to $x = - 2$

\begin{align*} x = -2 \amp \quad \text{ This equation has no slope, a vertical line } \\ \text{no slope } \amp\quad \text{ Perpendicular line then would have a zero slope } \\ m = 0 \amp\quad \text{ Use this and our point } (3, 4) \\ y - y_1 = m(x -x_1) \amp \quad \text{ Plug this information into point - slope formula } \\ y - 4=0(x - 3) \amp\quad \text{ Distribute slope } \\ y - 4= 0 \amp\quad \text{ Solve for } y \\ + 4+ 4 \amp \quad \text{ Add $4$ to each side } \\ y = 4 \amp\quad \text{ Our Solution } \end{align*}

Being aware that to be perpendicular to a vertical line means we have a horizontal line through a $y$ value of $4\text{,}$ thus we could have jumped from this point right to the solution, $y =4\text{.}$

Exercises Exercises - Parallel and Perpendicular Lines

Exercise Group.

Find the slope of a line parallel to each given line.

1.

$y = 2x +4 $

2.

$y = -\frac{2}{ 3} x + 5 $

3.

$y = 4x -5 $

4.

$y = -\frac{10}{3} x - 5 $

5.

$x - y = 4 $

6.

$6x - 5y = 20 $

7.

$7x + y = -2 $

8.

$3x +4y = -8 $

Exercise Group.

Find the slope of a line perpendicular to each given line.

9.

$x =3 $

10.

$y = -\frac{ 1 }{2} x -1 $

11.

$y = -\frac{ 1}{ 3} x $

12.

$y =\frac{ 4}{ 5} x $

13.

$x - 3y = -6 $

14.

$3x - y = - 3 $

15.

$x +2y =8 $

16.

$8x - 3y =-9 $

Exercise Group.

Write the point-slope form of the equation of the line described.

17.

through: $(2, 5)\text{,}$ parallel to $x =0 $

18.

through: $(5, 2)\text{,}$ parallel to $y = \frac{7}{ 5} x + 4 $

19.

through: $(3, 4)\text{,}$ parallel to $y =\frac{9}{ 2} x - 5 $

20.

through: $(1, - 1)\text{,}$ parallel to $y = -\frac{ 3}{ 4} x + 3 $

21.

through: $(2, 3)\text{,}$ parallel to $y = \frac{7}{ 5} x +4 $

22.

through: $( - 1, 3)\text{,}$ parallel to $y = - 3x -1 $

23.

through: $(4, 2)\text{,}$ parallel to $x =0 $

24.

through: $(1, 4)\text{,}$ parallel to $y = \frac{7}{ 5} x +2 $

25.

through: $(1, -5)\text{,}$ perpendicular to $- x + y =1 $

26.

through: $(1, - 2)\text{,}$ perpendicular to $-x +2y =2 $

27.

through: $(5, 2)\text{,}$ perpendicular to $5x + y = -3 $

28.

through: $(1, 3)\text{,}$ perpendicular to $- x + y = 1 $

29.

through: $(4, 2)\text{,}$ perpendicular to $- 4x + y = 0 $

30.

through: $( - 3, - 5)\text{,}$ perpendicular to $3x + 7y = 0 $

31.

through: $(2, - 2) \text{,}$ perpendicular to $3y -x =0 $

32.

through: $(- 2, 5) \text{,}$ perpendicular to $y - 2x =0 $

Exercise Group.

Write the slope-intercept form of the equation of the line described.

33.

through: $(4, - 3)\text{,}$ parallel to $y = -2x $

34.

through: $( - 5, 2)\text{,}$ parallel to $y =\frac{ 3}{ 5} x $

35.

through: $( - 3, 1)\text{,}$ parallel to $y = -\frac{ 4}{ 3} x - 1 $

36.

through: $( - 4, 0)\text{,}$ parallel to $y = -\frac{ 5}{ 4 }x + 4 $

37.

through: $( - 4, - 1)\text{,}$ parallel to $y = -\frac{1}{ 2} x + 1 $

38.

through: $(2, 3)\text{,}$ parallel to $y =\frac{ 5}{ 2} x - 1 $

39.

through: $( - 2, -1)\text{,}$ parallel to $y = -\frac{1}{ 2} x - 2 $

40.

through: $( - 5, -4)\text{,}$ parallel to $y =\frac{ 3}{ 5} x - 2 $

41.

through: $(4, 3)\text{,}$ perpendicular to $x + y = -1 $

42.

through: $( -3, - 5)\text{,}$ perpendicular to $x + 2y = -4 $

43.

through: $(5, 2)\text{,}$ perpendicular to $x = 0 $

44.

through: $(5, - 1)\text{,}$ perpendicular to $- 5x + 2y = 10 $

45.

through: $( - 2, 5)\text{,}$ perpendicular to $-x + y = -2 $

46.

through: $(2, - 3)\text{,}$ perpendicular to $-2x +5y = -10 $

47.

through: $(4, - 3)\text{,}$ perpendicular to $- x +2y = -6 $

48.

through: $( - 4, 1)\text{,}$ perpendicular to $4x +3y = - 9 $