Section 3.2 Compound Inequalities
Several inequalities can be combined together to form what are called compound inequalities. There are three types of compound inequalities which we will investi- gate in this lesson.
The first type of a compound inequality is an OR inequality. For this type of inequality we want a true statment from either one inequality OR the other inequality OR both. When we are graphing these type of inequalities we will graph each individual inequality above the number line, then move them both down together onto the actual number line for our graph that combines them together.
When we give interval notation for our solution, if there are two different parts to the graph we will put a \(\cup\) (union) symbol between two sets of interval notation, one for each part.
Example 3.2.1.
Solve each inequality, graph the solution, and give interval notation of solution.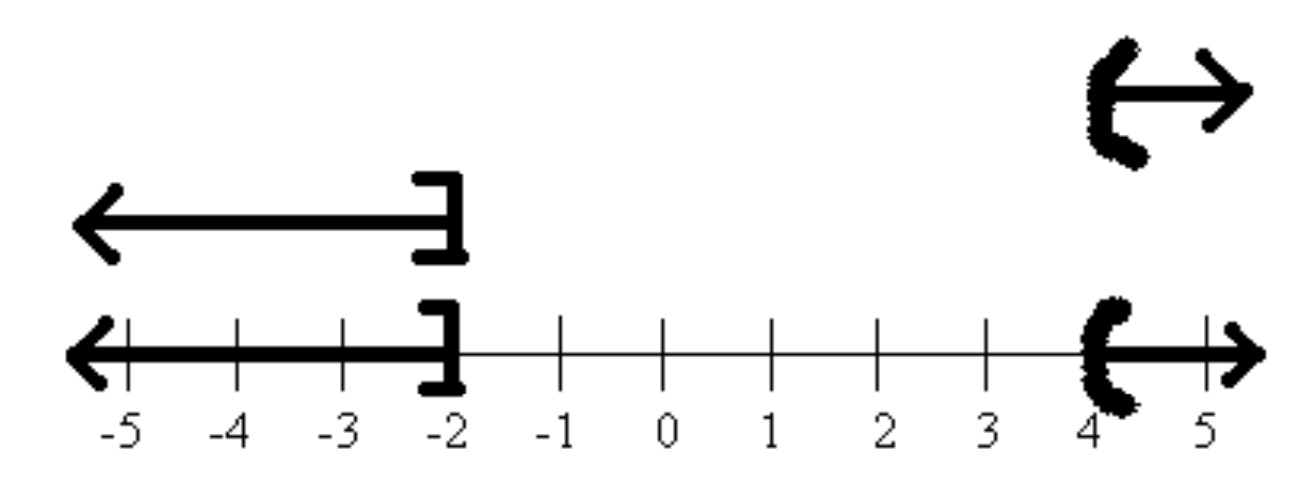
World View Note: The symbol for infinity was first used by the Romans, although at the time the number was used for \(1000\text{.}\) The greeks also used the symbol for \(10,000\text{.}\)
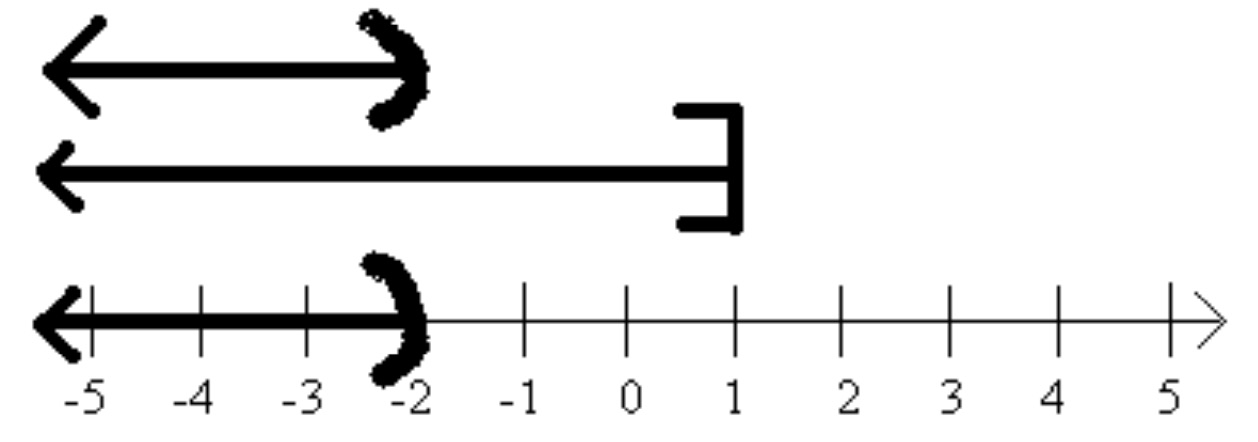
There are several different results that could result from an OR statement. The graphs could be pointing different directions, as in the graph above, or pointing in the same direction as in the graph below on the left, or pointing opposite direc- tions, but overlapping as in the graph below on the right. Notice how interval notation works for each of these cases.
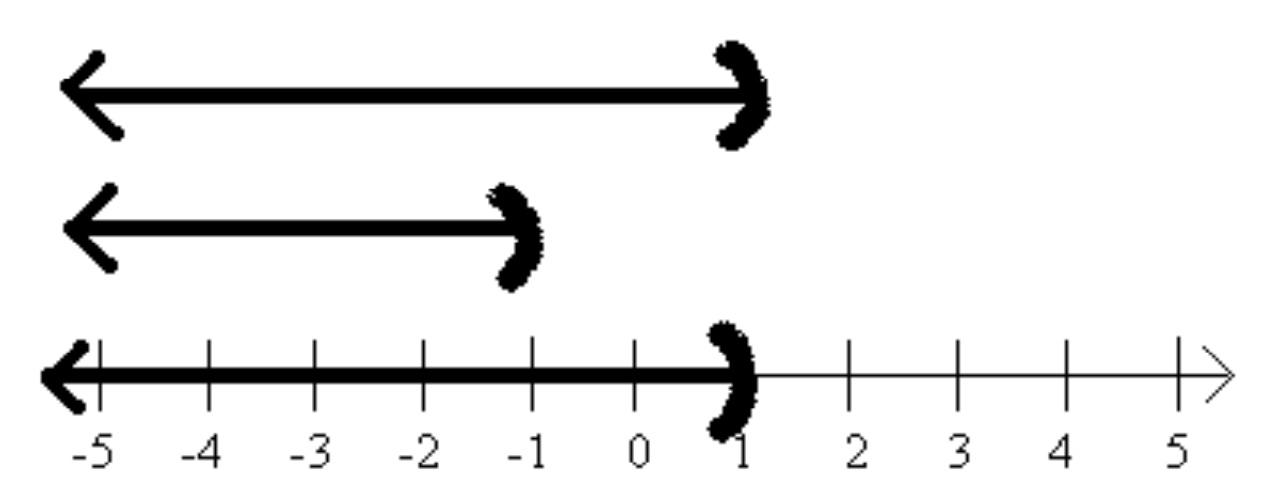
As the graphs overlap, we take the largest graph for our solution.
When the graphs are combined they cover the entire number line.
Interval Notation: \(\left(-\infty,1\right)\)
Interval Notation: \(\left(-\infty,\infty\right)\text{,}\) or \(\mathbb{R}\)
The second type of compound inequality is an AND inequality. AND inequalities require both statements to be true. If one is false, they both are false. When we graph these inequalities we can follow a similar process, first graph both inequali- ties above the number line, but this time only where they overlap will be drawn onto the number line for our final graph. When our solution is given in interval notation it will be expressed in a manner very similar to single inequalities (there is a symbol that can be used for AND, the intersection - \(\cap\) , but we will not use it here).
Example 3.2.2.
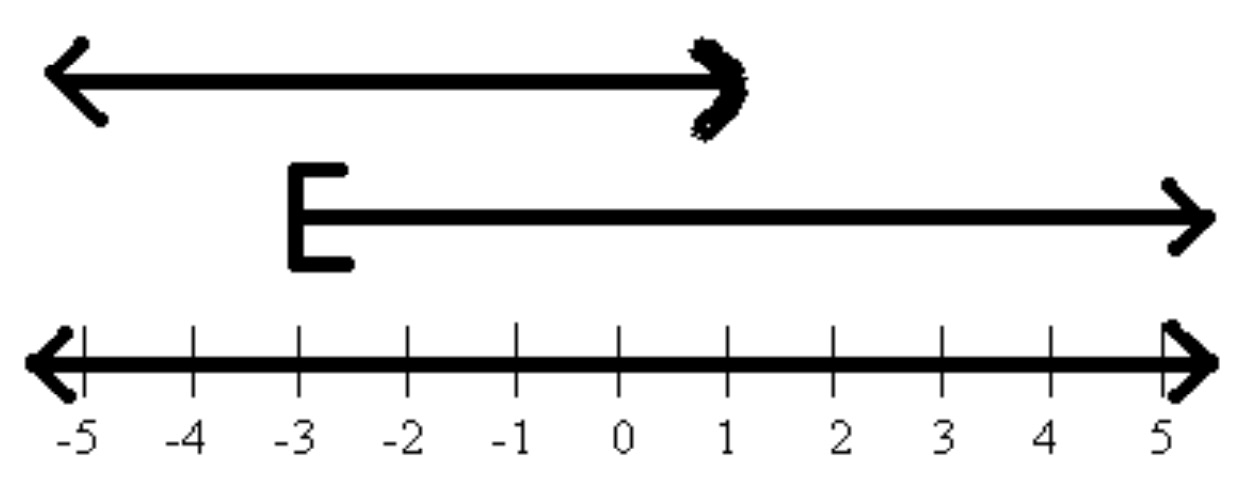
Solve each inequality, graph the solution, and express it interval notation.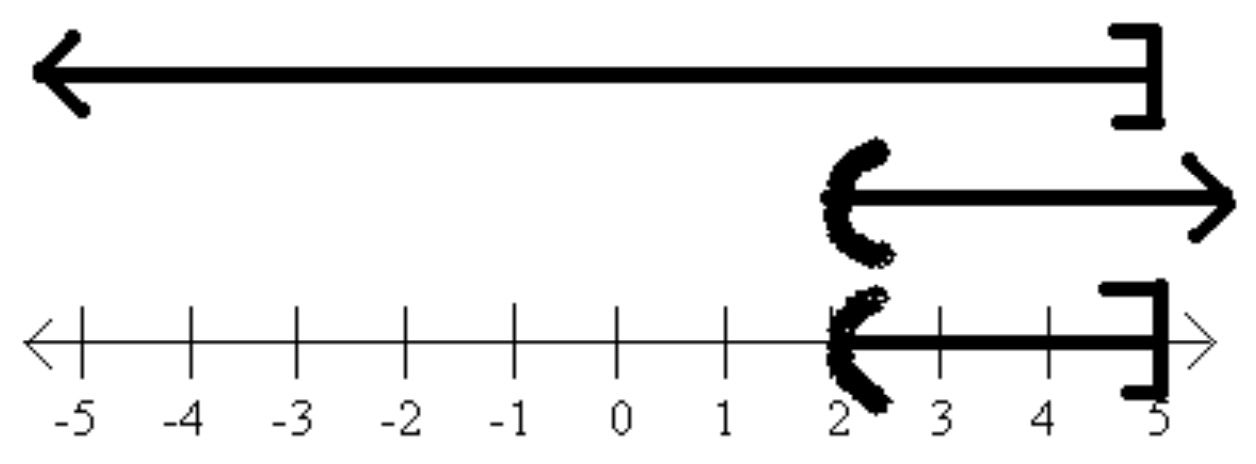
Again, as we graph AND inequalities, only the overlapping parts of the individual graphs makes it to the final number line. As we graph AND inequalities there are also three different types of results we could get. The first is shown in the above example. The second is if the arrows both point the same way, this is shown below on the left. The third is if the arrows point opposite ways but don’t overlap, this is shown below on the right. Notice how interval notation is expressed in each case.
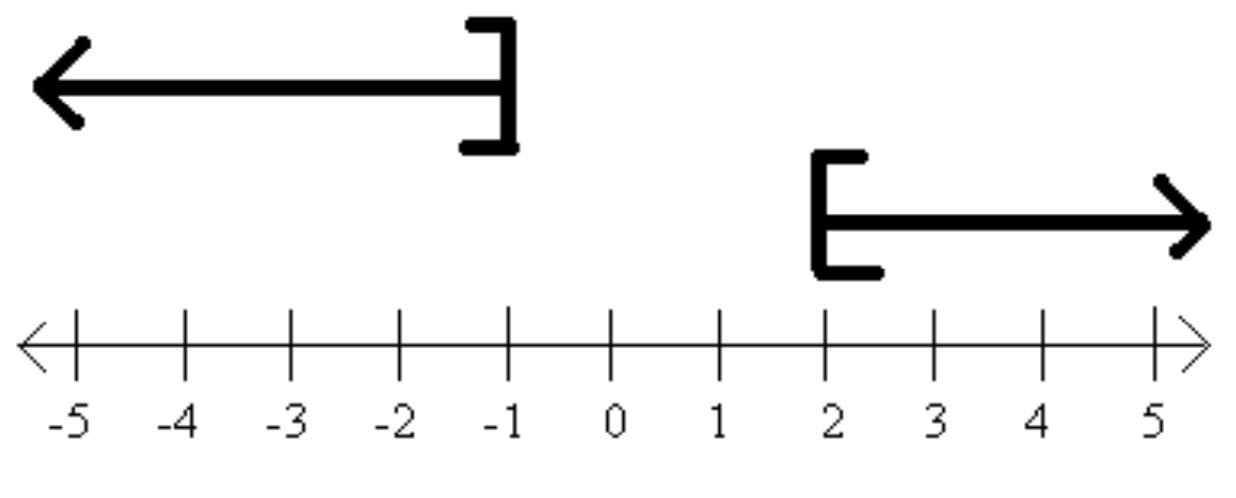
In this graph, the overlap is only the smaller graph, so this is what makes it to the final number line.
In this graph there is no overlap of the parts. Because their is no overlap, no values make it to the final number line.
Interval Notation: \(\left(-\infty,-2\right)\)
Interval Notation: No Solution or \(\emptyset \)
The third type of compound inequality is a special type of AND inequality. When our variable (or expression containing the variable) is between two numbers, we can write it as a single math sentence with three parts, such as \(5\lt x \leq 8\text{,}\) to show \(x\) is between \(5\) and \(8\) (or equal to \(8\)). When solving these type of inequalities, because there are three parts to work with, to stay balanced we will do the same thing to all three parts (rather than just both sides) to isolate the variable in the middle. The graph then is simply the values between the numbers with appropriate brackets on the ends.
Example 3.2.3.
Solve the inequality, graph the solution, and give interval notation.
Exercises Exercises - Compound Inequalities
Exercise Group.
Solve each compound inequality, graph its solution, and give interval notation.
1.
\(\frac{n}{3}\leq-3\text{ or } -5n\leq-10\)
2.
\(6m\ge -24\text{ or } m-7\lt -12\)
3.
\(x+7\geq12\text{ or } 9x\lt -45 \)
4.
\(10r\gt 0\text{ or } r-5\lt-12\)
5.
\(x-6\lt-13\text{ or }6x\leq -60\)
6.
\(9+n\lt 2\text{ or } 5n\gt 40\)
7.
\(\frac{v}{8}\gt -1\text{ and } v-2\lt 2\)
8.
\(-9x\lt 63\text{ and }\frac{x}{4}\lt 1 \)
9.
\(-8+b\lt -3 \text{ and } 4b\lt 20 \)
10.
\(-6n\leq 12\text{ and } \frac{n}{3}\leq 2 \)
11.
\(a+10\geq 3\text{ and } 8a\leq 48 \)
12.
\(-6+v\geq 0 \text{ and } 2v\gt4 \)
13.
\(3\leq9+x\leq7\)
14.
\(0\geq \frac{x}{9}\geq-1\)
15.
\(11\lt8+k\leq12 \)
16.
\(-11\leq n-9\leq-5 \)
17.
\(-3\lt x-1\lt 1 \)
18.
\(1\leq\frac{p}{8}\leq 0 \)
19.
\(-4\lt 8-3m\leq 11 \)
20.
\(3+7r\gt 59\text{ or } -6r-3\gt 33\)
21.
\(-16\leq 2n-10\leq -22\)
22.
\(-6-8x\geq -6\text{ or }2+10x\gt 82 \)
23.
\(-5b+10\leq 30\text{ and } 7b+2 \leq -40 \)
24.
\(n+10 \geq 15 \text{ or } 4n-5\lt-1 \)
25.
\(3x-9 \lt 2x+10 \text{ and } 5+7x \leq 10x-10 \)
26.
\(4n+8 \lt 3n-6 \text{ or } 10n-8 \geq 9+9n \)
27.
\(-8-6v\leq8-8v\text{ and }7v+9\leq6+10v \)
28.
\(5-2a\geq2a+1\text{ or }10a-10\geq9a+9 \)
29.
\(1+5k\leq7k-3\text{ or }k-10\gt2k+10\)
30.
\(8-10r\leq8+4r\text{ or }-6+8r\lt2+8r\)
31.
\(2x+9\geq10x+1\text{ and }3x-2\lt 7x+2 \)
32.
\(-9m+2\lt-10-6m\text{ or } -m+5\geq10+4m \)