College Preparatory Mathematics

Section 3.3 Absolute Value Inequalities

When an inequality has an absolute value we will have to remove the absolute value in order to graph the solution or give interval notation. The way we remove the absolute value depends on the direction of the inequality symbol.

Consider \(|x| \lt 2\text{.}\)

Absolute value is defined as distance from zero. Another way to read this inequality would be the distance from zero is less than \(2\text{.}\) So on a number line we will shade all points that are less than \(2\) units away from zero.

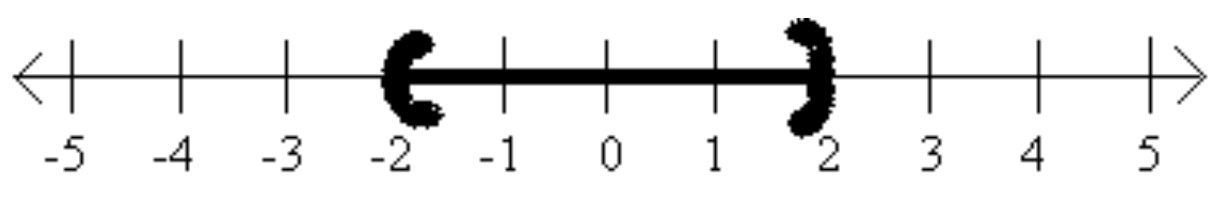
Consider \(|x| \gt 2\text{.}\)

Absolute value is defined as distance from zero. Another way to read this inequality would be the distance from zero is greater than \(2\text{.}\) So on the number line we shade all points that are more than \(2\) units away from zero.

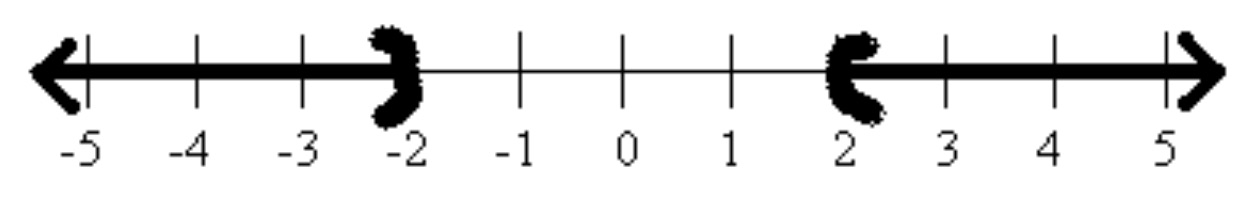
World View Note: The phrase “absolute value” comes from German mathematician Karl Weierstrass in \(1876\text{,}\) though he used the absolute value symbol for complex numbers. The first known use of the symbol for integers comes from a \(1939\) edition of a college algebra text!

For all absolute value inequalities we can also express our answers in interval notation which is done the same way it is done for standard compound inequalities.

We can solve absolute value inequalities much like we solved absolute value equa- tions. Our first step will be to isolate the absolute value. Next we will remove the absolute value by making a three part inequality if the absolute value is less than a number, or making an OR inequality if the absolute value is greater than a number. Then we will solve these inequalites. Remember, if we multiply or divide by a negative the inequality symbol will switch directions!

Example 3.3.1.

Solve, graph, and give interval notation for the solution.

\begin{align*} |4x-5|\geq 6 \amp \quad \text{ Absolute value is greater, use OR } \\ 4x-5\geq 6 \text{ OR } 4x-5\leq -6 \amp\quad \text{ Solve } \\ +5\quad +5 \qquad +5\quad +5 \amp\quad \text{ Add $5$ to both sides } \\ 4x\geq 11 \text{ OR } 4x\leq -1 \amp\quad \text{ Divide both sides by } 4 \\ \frac{4x}{4}\geq \frac{11}{4} \text{ OR } \frac{4x}{4}\leq \frac{-1}{4} \amp\quad \text{ } \\ x\geq \frac{11}{4}\text{ OR } x\leq -\frac{1}{4} \amp\quad \text{ Graph } \end{align*}

\begin{align*} \left(-\infty,-\frac{1}{4}\right]\cup\left[\frac{11}{4},\infty\right) \amp\quad \text{ Interval notation } \end{align*}

Example 3.3.2.

Solve, graph, and give interval notation for the solution.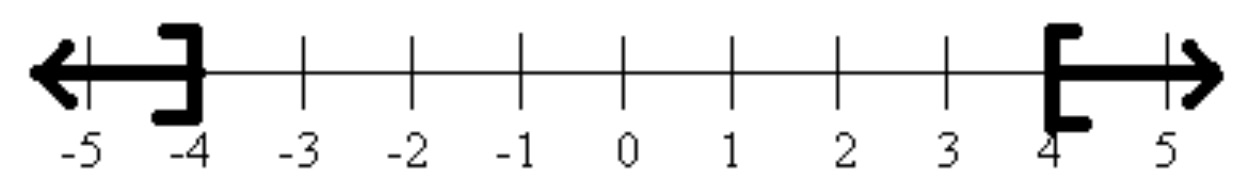

\begin{align*} -4-3|x|\leq -16 \amp \quad \text{ Add $4$ to both sides } \\ +4\qquad \qquad +4 \amp\quad \text{ } \\ -3|x|\leq -12 \amp\quad \text{ Divide both sides by } -3 \\ \frac{-3|x|}{-3}\geq \frac{-12}{-3} \amp\quad \text{ Dividing by a negative switches the symbol } \\ |x|\geq 4 \amp\quad \text{ Absolute value is greater, use OR } \\ x\geq 4 \text{ OR } x\leq -4 \amp\quad \text{ Graph } \end{align*}

\begin{align*} \left(-\infty,-4\right]\cup\left[ 4,\infty\right) \amp\quad \text{ Interval Notation } \end{align*}

In the previous example, we cannot combine \(-4\) and \(-3\) because they are not like terms, the \(-3\) has an absolute value attached. So we must first clear the \(-4\) by adding \(4\text{,}\) then divide by \(-3\text{.}\) The next example is similar.

Example 3.3.3.

Solve, graph, and give interval notation for the solution.

\begin{align*} 9-2|4x+1|\gt 3 \amp \quad \text{ Subtract $9$ from both sides } \\ -9 \qquad \qquad \quad -9 \amp\quad \text{ } \\ -2|4x+1|\gt -6 \amp\quad \text{ Divide both sides by } -2 \\ \frac{-2|4x+1|}{-2}\lt \frac{-6}{-2} \amp\quad \text{ Dividing by negative switches the symbol } \\ |4x+1|\lt 3 \amp\quad \text{ Absolute value is less, use three part } \\ -3\lt 4x+1 \lt 3 \amp\quad \text{ Solve } \\ -1\qquad -1\ -1 \amp\quad \text{ Subtract $1$ from all three parts } \\ -4\lt 4x \lt 2 \amp\quad \text{ Divide all three parts by } 4 \\ \frac{-4}{4}\lt \frac{4x}{4} \lt \frac{2}{4} \amp\quad \text{ } \\ -1\lt x\lt \frac{1}{2} \amp\quad \text{ Graph } \end{align*}

\begin{align*} \left(-1,\frac{1}{2}\right) \amp\quad \text{ Interval notation } \end{align*}

In the previous example, we cannot distribute the \(-2\) into the absolute value. We can never distribute or combine things outside the absolute value with what is inside the absolute value. Our only way to solve is to first isolate the absolute value by clearing the values around it, then either make a compound inequality (and OR or a three part) to solve.

It is important to remember as we are solving these equations, the absolute value is always positive. If we end up with an absolute value is less than a negative number, then we will have no solution because absolute value will always be positive, greater than a negative. Similarly, if absolute value is greater than a negative, this will always happen. Here the answer will be all real numbers.

Example 3.3.4.

Solve, graph, and give interval notation for the solution.

\begin{align*} 12 + 4|6x - 1| \lt 4 \amp \quad \text{ Subtract $12$ from both sides } \\ -12\qquad\qquad -12 \amp\quad \text{ } \\ 4|6x-1|\lt -8 \amp\quad \text{ } \\ \frac{4|6x-1|}{4}\lt \frac{-8}{4} \amp\quad \text{ Divide both sides by } 4 \\ |6x - 1| \lt - 2 \amp\quad \text{ Absolute value can't be less than a negative } \end{align*}

\begin{gather*} \text{ No solution or } \emptyset \end{gather*}

Example 3.3.5.

Solve, graph, and give interval notation for the solution.

\begin{align*} 5 - 6|x + 7| \leq 17 \amp \quad \text{ Subtract $5$ from both sides } \\ -5\qquad\qquad -5 \amp\quad \text{ } \\ - 6|x + 7| \leq 12 \amp\quad \text{ Divide both sides by } -6 \\ \frac{- 6|x + 7|}{-6}\geq \frac{12}{-6} \amp\quad \text{Dividing by a negative flips the symbol } \\ |x + 7| \geq - 2 \amp\quad \text{ Absolute valuealways greater than negative } \end{align*}

\begin{gather*} \left(-\infty,\infty\right) \text{ All real numbers of } {\mathbb R} \end{gather*}