Solve and Graph Inequalities

Section 3.1 Solve and Graph Inequalities

Objective: Solve, graph, and give interval notation for the solution to linear inequalities.

When we have an equation such as $x = 4$ we have a specific value for our variable. With inequalities we will give a range of values for our variable. To do this we will not use equals, but one of the following symbols:

\begin{align*} \gt \amp \quad \text{Greater than} \\ \geq \amp\quad \text{Greater then or equal to} \\ \lt \amp\quad \text{Less than} \\ \leq \amp\quad \text{Less than or equal to} \end{align*}

World View Note: English mathematician Thomas Harriot first used the above symbols in $1631\text{.}$ However, they were not immediately accepted as symbols such as $\sqsubset$ and $\sqsupset$ were already coined by another English mathematician, William Oughtred.

If we have an expression such as $x \lt 4\text{,}$ this means our variable can be any number smaller than $4$ such as $-2, 0, 3, 3.9 $ or even $3.999999999$ as long as it is smaller than $4\text{.}$ If we have an expression such as $x\geq -2\text{,}$ this means our variable can be any number greater than or equal to $-2\text{,}$ such as $5, 0, -1, -1.9999\text{,}$ or even $-2\text{.}$

Because we don’t have one set value for our variable, it is often useful to draw a picture of the solutions to the inequality on a number line. We will start from the value in the problem and bold the lower part of the number line if the variable is smaller than the number, and bold the upper part of the number line if the variable is larger. The value itself we will mark with brackets, either $) $ or $($ for less than or greater than respectively, and $]$ or $[$ for less than or equal to or greater than or equal to respectively.

Once the graph is drawn we can quickly convert the graph into what is called interval notation. Interval notation gives two numbers, the first is the smallest value, the second is the largest value. If there is no largest value, we can use $\infty $ (infinity). If there is no smallest value, we can use $-\infty $ negative infinity. If we use either positive or negative infinity we will always use a curved bracket for that value.

Example 3.1.1.

Graph the inequality and give the interval notation.

\begin{align*} x\lt 2 \amp \quad \text{ Start at $2$ and shade below } \\ \amp\quad \text{ Use $)$ for less than } \end{align*}

Our Graph

\begin{align*} (-\infty,2) \amp\quad \text{ Interval Notation } \end{align*}

Example 3.1.2.

Graph the inequality and give the interval notation.

\begin{align*} x\geq -1 \amp \quad \text{ Start at $-1$ and shade above } \\ \amp\quad \text{ Use $[$ for greater than or equal to} \end{align*}

Our Graph

\begin{align*} [-1,\infty) \amp\quad \text{ Interval Notation } \end{align*}

We can also take a graph and find the inequality for it.

Example 3.1.3.

Give the inequality for the graph:

Graph starts at $3$ and goes up or greater. Curved bracket means just greater than

\begin{align*} x\gt 3 \amp\quad \text{Our Solution} \end{align*}

Example 3.1.4.

Give the inequality for the graph:

Graph starts at $-4$ and goes down or less. Square bracket means less than or equal to

\begin{align*} x\leq -4 \amp\quad \text{Our Solution} \end{align*}

Generally when we are graphing and giving interval notation for an inequality we will have to first solve the inequality for our variable. Solving inequalities is very similar to solving equations with one exception. Consider the following inequality and what happens when various operations are done to it. Notice what happens to the inequality sign as we add, subtract, multiply and divide by both positive and negative numbers to keep the statment a true statement.

\begin{align*} 3\gt 1 \amp\quad \text{Add $3$ to both sides}\\ 6\gt 4 \amp\quad \text{Subtract $2$ from both sides}\\ 4\gt 2 \amp\quad \text{Multiply both sides by } 3\\ 12\gt 6 \amp\quad \text{Divide both sides by } 2 \\ 6\gt 3 \amp\quad \text{Add $-1$ to both sides} \\ 5\gt 2 \amp\quad \text{Subtract $-4$ from both sides}\\ 9\gt 6 \amp\quad \text{Multiply both sides by } -2\\ -18\lt -12 \amp\quad \text{Divide both sides by } -6\\ 3\gt 2 \amp\quad \text{Symbol flipped when we multiply or divide by a negative! } \end{align*}

As the above problem illustrates, we can add, subtract, multiply, or divide on both sides of the inequality. But if we multiply or divide by a negative number, the symbol will need to flip directions. We will keep that in mind as we solve inequalities.

Example 3.1.5.

Solve and give interval notation.

\begin{align*} 5-2x\geq 11 \amp \quad \text{Subtract $5$ from both sides} \\ -5\qquad -5 \amp\quad \text{ } \\ -2x\geq 6 \amp\quad \text{Divide both sides by } -2 \\ \frac{-2x}{-2}\leq \frac{6}{-2} \amp\quad \text{Divide by a negative - flip symbol! } \\ x\leq -3 \amp\quad \text{Graph, starting at $-3$, going down with $]$ for less than or equal to} \end{align*}

\begin{align*} (-\infty,-3] \amp\quad \text{ Interval Notation } \end{align*}

The inequality we solve can get as complex as the linear equations we solved. We will use all the same patterns to solve these inequalities as we did for solving equations. Just remember that any time we multiply or divide by a negative the symbol switches directions (multiplying or dividing by a positive does not change the symbol!)

Example 3.1.6.

Solve and give interval notation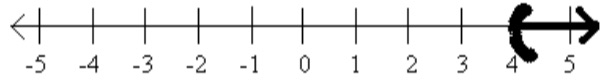

\begin{align*} 3(2x-4)+4x\lt 4(3x-7)+8 \amp \quad \text{Distribute } \\ 6x-12+4x\lt 12x-28+8 \amp\quad \text{ Combine like terms } \\ 10x-12\lt 12x-20 \amp\quad \text{Move variable to one side} \\ -10x\qquad -10x\qquad \amp\quad \text{ Subtract $10x$ from both sides } \\ -12\lt 2x-20 \amp\quad \text{ Add $20$ to both sides } \\ +20\qquad +20 \amp\quad \text{ } \\ 8\lt 2x \amp\quad \text{ } \\ \frac{8}{2}\lt \frac{2x}{2} \amp\quad \text{ Divide both sides by } 2 \\ 4\lt x \amp\quad \text{Be careful with graph, $x$ is larger! } \end{align*}

\begin{align*} (4,\infty) \amp\quad \text{ Interval Notation } \end{align*}

It is important to be careful when the inequality is written backwards as in the previous example ($4 \lt x$ rather than $x \gt 4$). Often students draw their graphs the wrong way when this is the case. The inequality symbol opens to the variable, this means the variable is greater than $4\text{.}$ So we must shade above the $4\text{.}$

Exercises Exercises - Solve and Graph Inequalities

Exercise Group.

Draw a graph for each inequality and give interval notation.

1.

$n\gt -5 $

2.

$n\gt 4 $

3.

$-2\geq k $

4.

$1\geq k $

5.

$5\geq x $

6.

$-5\lt x $

Exercise Group.

Write an inequality for each graph.

7.

8.

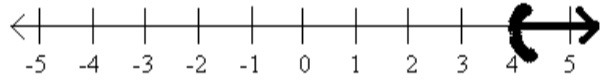
9.

10.

11.

12.

Exercise Group.

Solve each inequality, graph each solution, and give interval notation.

13.

$\frac{x}{11}\geq 10 $

14.

$-2\leq \frac{n}{13} $

15.

$2+r\lt 3 $

16.

$\frac{m}{5}\leq -\frac{6}{5} $

17.

$8+\frac{n+3}\geq 6 $

18.

$1 1 \gt 8 + \frac{x}{2} $

19.

$2\gt \frac{a-2}{5} $

20.

$\frac{v-9}{-4}\leq 2 $

21.

$-47\geq 8-5x $

22.

$\frac{6+x}{12}\leq -1 $

23.

$-2(3+k)\lt -44 $

24.

$-7n-10\geq 60 $

25.

$18\lt -2(-8+p) $

26.

$5\geq\frac{x}{5} + 1 $

27.

$24\geq -6(m-6) $

28.

$-8(n-5)\geq 0 $

29.

$-r-5(r-6)\lt -18 $

30.

$-60\geq -4(-6x-3) $

31.

$24+4b\lt 4(1+6b) $

32.

$-8(2-2n)\geq -16+n $

33.

$-5v-5\lt -5(4v+1) $

34.

$-36+6x\gt -8(x+2)+4x $

35.

$4+2(a+5)\lt -2(-a-4) $

36.

$3(n+3)+7(8-8n)\lt 5n+5+2 $

37.

$-(k-2)\gt -k-20 $

38.

$-(4-5p)+3\geq -2(8-5p) $