College Preparatory Mathematics

Section 4.1 Graphing

We have solved problems like \(3x - 4 = 11\) by adding \(4\) to both sides and then dividing by \(3\) (solution is \(x = 5\)). We also have methods to solve equations with more than one variable in them. It turns out that to solve for more than one variable we will need the same number of equations as variables. For example, to solve for two variables such as x and y we will need two equations. When we have several equations we are using to solve, we call the equations a system of equations. When solving a system of equations we are looking for a solution that works in both equations. This solution is usually given as an ordered pair \((x, y)\text{.}\) The following example illustrates a solution working in both equations

As we found a true statement for both equations we know \((2,1)\) is the solution to the system. It is in fact the only combination of numbers that works in both equations. In this lesson we will be working to find this point given the equations. It seems to follow that if we use points to describe the solution, we can use graphs to find the solutions.

If the graph of a line is a picture of all the solutions, we can graph two lines on the same coordinate plane to see the solutions of both equations. We are interested in the point that is a solution for both lines, this would be where the lines intersect! If we can find the intersection of the lines we have found the solution that works in both equations.

Example 4.1.2.

\begin{align*} \begin{matrix} y=-\frac{1}{2}x+3 \\ y = \frac{3}{4} x - 2 \end{matrix} \amp\quad \text{ To graph we identify slopes and $y$-intercepts }\\ \\ \begin{matrix} \text{First: } m=-\frac{1}{2},\ b=3 \\ \text{Second: } m=\frac{3}{4},\ b=-2 \end{matrix} \amp\quad \text{ Now we can graph both lines on the same plane. } \end{align*}

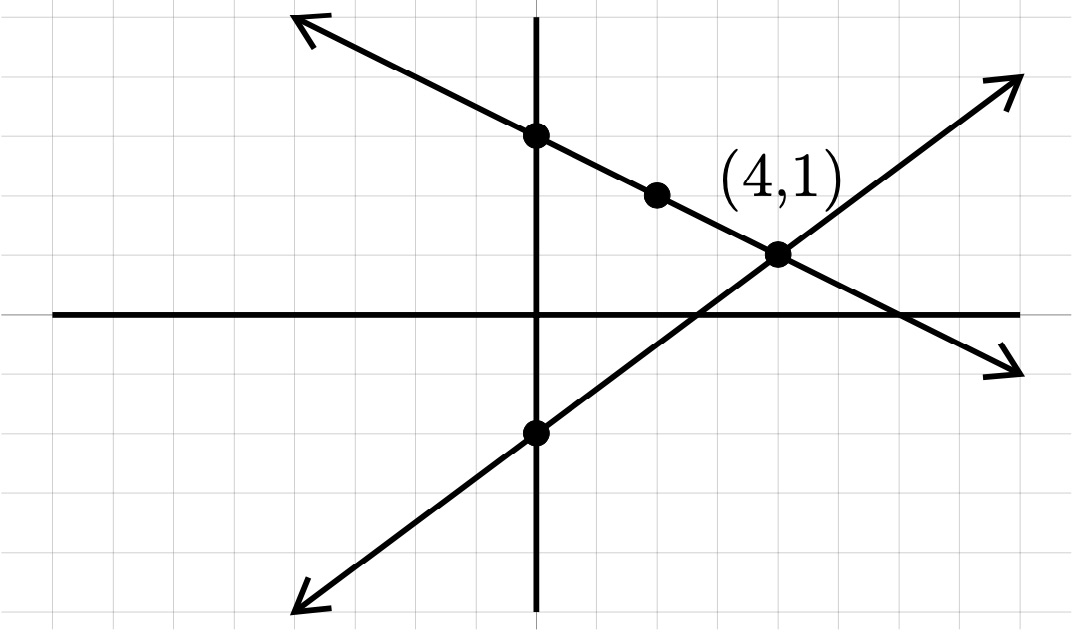
To graph each equation, we start at the \(y\)-intercept and use the slope \(\frac{\text{rise}}{\text{run}}\) to get the next point and connect the dots.

Remember a negative slope is downhill!

Find the intersection point, \((4,1)\)

\((4,1)\) Our Solution

Often our equations won’t be in slope-intercept form and we will have to solve both equations for \(y\) first so we can idenfity the slope and \(y\)-intercept.

Example 4.1.3.

\begin{align*} \begin{matrix} 6x-3y=-9 \\ 2x+2y=-6 \end{matrix} \amp\quad \text{Solve each equation for } y \\ \\ 6x-3y=-9 \quad 2x+2y=-6 \amp \quad \text{ } \\ -6x \qquad -6x\quad -2x \qquad-2x \amp\quad \text{ Subtract $x$ terms } \\ -3y=-6x-9\quad 2y=-2x-6 \amp\quad \text{ Put $x$ terms first } \\ \frac{-3y}{-3}=\frac{-6x-9}{-3}\quad \frac{2y}{2}=\frac{-2x-6}{2} \amp \quad \text{ Divide by coefficient of } y \\ y = 2x + 3 \qquad y = - x - 3 \amp\quad \text{ Identify slope and $y$ - intercepts } \\ \\ \begin{matrix} \text{First: } m=\frac{2}{1},\ b=3 \\ \text{Second: } m=-\frac{1}{1},\ b=-3 \end{matrix} \amp\quad \text{ Now we can graph both lines on the same plane. } \end{align*}

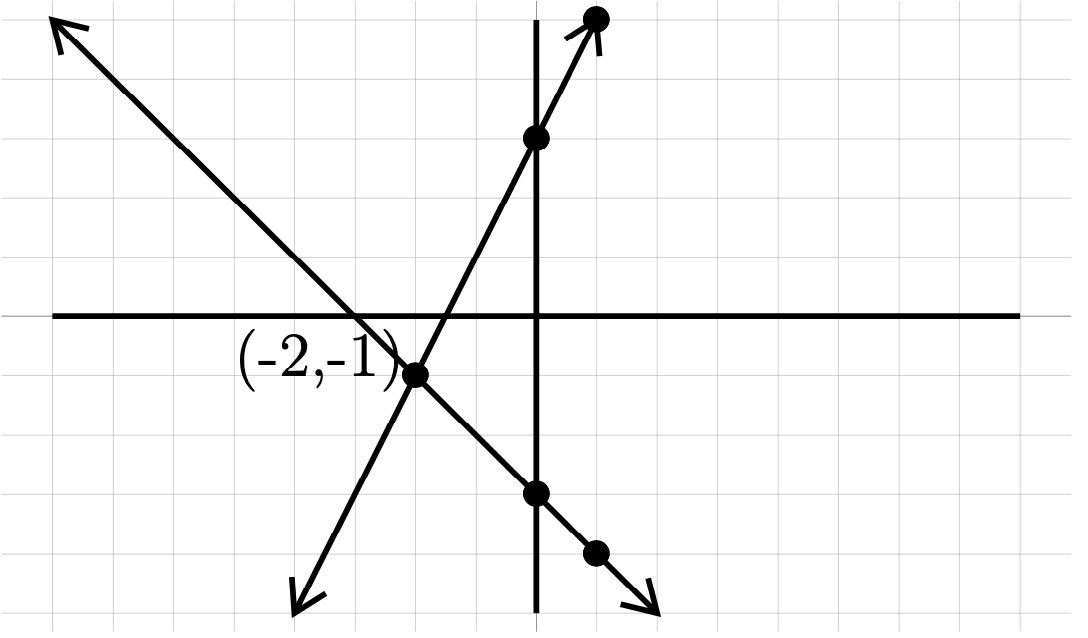
To graph each equation, we start at the \(y\)-intercept and use the slope \(\frac{\text{rise}}{\text{run}}\) to get the next point and connect the dots.

Remember a negative slope is downhill!

Find the intersection point, \((-2,-1)\)

\((-2,-1)\) Our Solution

As we are graphing our lines, it is possible to have one of two unexpected results. These are shown and discussed in the next two example.

Example 4.1.4.

\begin{align*} \begin{matrix} y = \frac{3}{2} x - 4\\ y = \frac{3}{2} x + 1 \end{matrix} \amp\quad \text{ Identify slope and $y$ - intercept of each equation. } \\ \\ \begin{matrix} \text{First: } m=\frac{3}{2},\ b=-4 \\ \text{Second: } m=\frac{3}{2},\ b=1 \end{matrix} \amp\quad \text{ Now we can graph both lines on the same plane.} \end{align*}

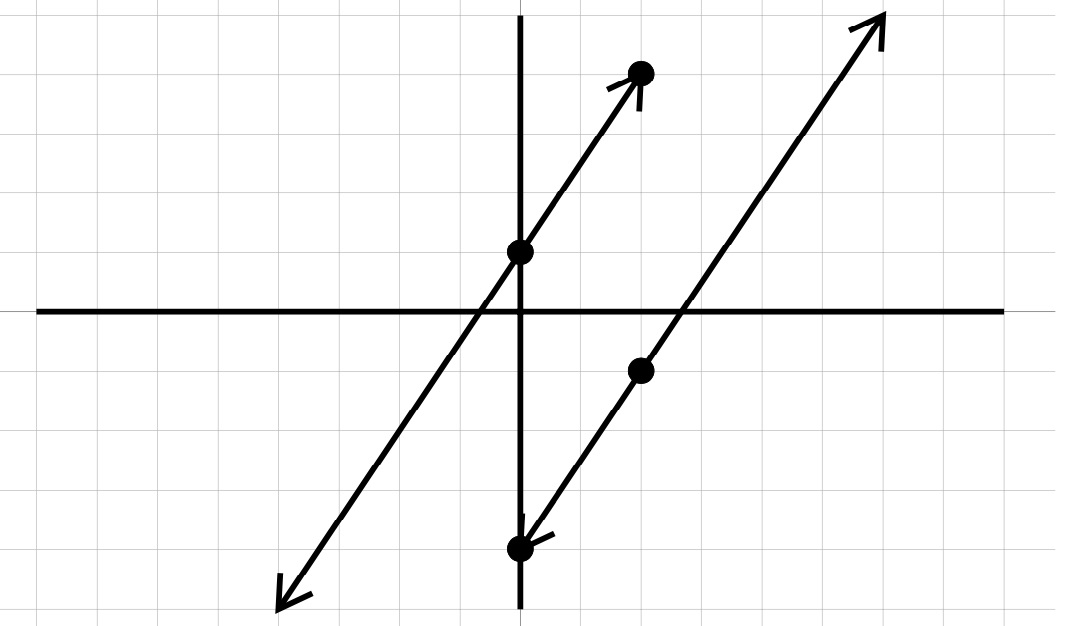
To graph each equation, we start at the \(y\)-intercept and use the slope \(\frac{\text{rise}}{\text{run}}\) to get the next point and connect the dots.

The two lines do not intersect! They are parallel! If the lines do not intersect we know that there is no point that works in both equations, there is no solution

\(\emptyset\) No solution

We also could have noticed that both lines had the same slope. Remembering that parallel lines have the same slope we would have known there was no solution even without having to graph the lines.

Example 4.1.5.

\begin{align*} \begin{matrix} 2x-6y=12 \\ 3x-9y=18\end{matrix} \amp\quad \text{ Solve each equation for } y \\ \\ 2x-6y=12 \quad 3x-9y=18 \amp \quad \text{ } \\ -2x \qquad -2x\quad -3x\qquad -3x \amp\quad \text{ Subtract $x$ terms } \\ -6y=-2x+12 \quad -9y=-3x+18 \amp\quad \text{ Put $x$ terms first } \\ \frac{-6y}{-6}=\frac{-2x+12}{-6} \quad \frac{-9y}{-9}=\frac{-3x+18}{-9} \amp \quad \text{ Divide by coefficient of } y \\ y = \frac{1}{3}x -2 \qquad y = \frac{1}{3} x - 2 \amp\quad \text{ Identify slope and $y$ - intercepts } \\ \\ \begin{matrix} \text{First: } m=\frac{1}{3},\ b=-2 \\ \text{Second: } m=\frac{1}{3},\ b=-2 \end{matrix} \amp\quad \text{ Now we can graph both lines on the same plane. } \end{align*}

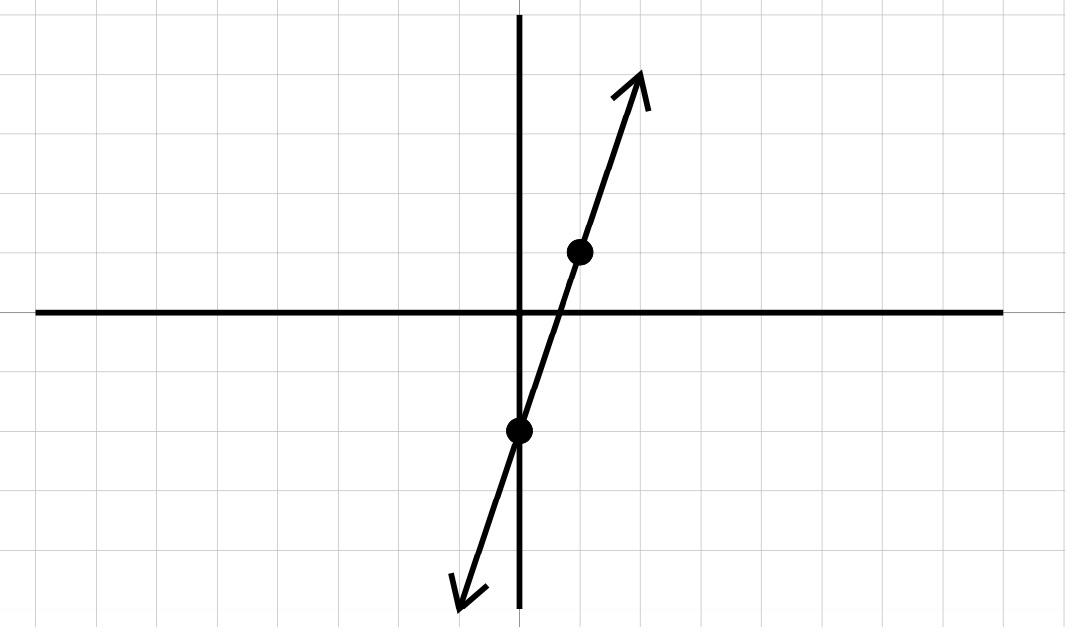
To graph each equation, we start at the \(y\)-intercept and use the slope \(\frac{\text{rise}}{\text{run}}\) to get the next point and connect the dots.

Both equations are the same line! As one line is directly on top of the other line, we can say that the lines “intersect” at all the points! Here we say we have infinite solutions.

Once we had both equations in slope-intercept form we could have noticed that the equations were the same. At this point we could have stated that there are infinite solutions without having to go through the work of graphing the equations.

World View Note: The Babylonians were the first to work with systems of equations with two variables. However, their work with systems was quickly passed by the Greeks who would solve systems of equations with three or four variables and around \(300\) AD, developed methods for solving systems with any number of unknowns!